Suppose that two cards are drawn at random from a deck of cards.

Let X denote the number of aces obtained. Therefore, X can take any of the values of 0, 1, or 2.

In a deck of 52 cards, 4 cards are aces. Therefore, there are 48 non-ace cards.

$\therefore \mathrm{P}(\mathrm{X}=0)=\mathrm{P}(0$ ace and 2 non-ace cards $)=\frac{{ }^{4} \mathrm{C}_{0} \times{ }^{48} \mathrm{C}_{2}}{{ }^{52} \mathrm{C}_{2}}=\frac{1128}{1326}$

$P(X=1)=P(1$ ace and 1 non-ace cards $)=\frac{{ }^{4} C_{1} \times{ }^{48} C_{1}}{{ }^{52} C_{2}}=\frac{192}{1326}$

$P(X=2)=P(2$ ace and 0 non- ace cards $)=\frac{{ }^{4} C_{2} \times{ }^{48} C_{0}}{{ }^{52} C_{2}}=\frac{6}{1326}$

Thus, the probability distribution is as follows.

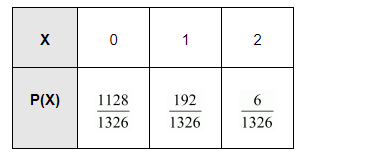
Then, $\mathrm{E}(\mathrm{X})=\sum p_{i} x_{i}$

$=0 \times \frac{1128}{1326}+1 \times \frac{192}{1326}+2 \times \frac{6}{1326}$

$=\frac{204}{1326}$

$=\frac{2}{13}$

Therefore, the correct answer is D.