The area between

The line, $x=a$, divides the area bounded by the parabola and $x=4$ into two equal parts.

$\therefore$ Area $\mathrm{OAD}=$ Area $\mathrm{ABCD}$

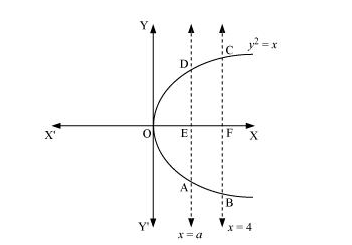
It can be observed that the given area is symmetrical about x-axis.

⇒ Area OED = Area EFCD

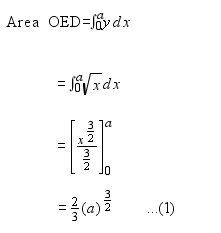
Area of EFCD $=\int_{a}^{4} \sqrt{x} d x$

$=\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{a}^{4}$

$=\frac{2}{3}\left[8-a^{\frac{3}{2}}\right]$               ...(2)

From (1) and (2), we obtain

$\frac{2}{3}(a)^{\frac{3}{2}}=\frac{2}{3}\left[8-(a)^{\frac{3}{2}}\right]$

$\Rightarrow 2 \cdot(a)^{\frac{3}{2}}=8$

$\Rightarrow(a)^{\frac{3}{2}}=4$

$\Rightarrow a=(4)^{\frac{2}{3}}$

Therefore, the value of $a$ is $(4)^{\frac{2}{3}}$.