Question:
The area (in sq. units) of an equilateral triangle inscribed in the parabola $y^{2}=8 x$, with one of its vertices on the vertex of this parabola, is:
Correct Option: , 3
Solution:
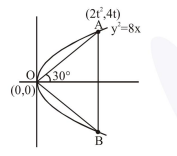
$\tan 30^{\circ}=\frac{4 \mathrm{t}}{2 \mathrm{t}^{2}}=\frac{2}{\mathrm{t}} \Rightarrow \mathrm{t}=2 \sqrt{3}$
$\mathrm{AB}=8 \mathrm{t}=16 \sqrt{3}$
Area $=256.3 \cdot \frac{\sqrt{3}}{4}=192 \sqrt{3}$
