Question:
The area (in sq. units) of the region
$\left\{(x, y): 0 \leq y \leq x^{2}+1,0 \leq y \leq x+1, \frac{1}{2} \leq x \leq 2\right\}$ is :
Correct Option: , 2
Solution:
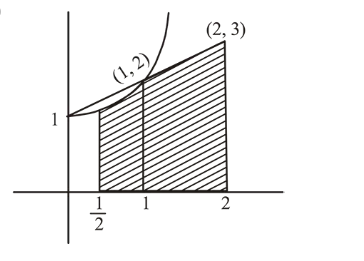
Required area $=\int_{\frac{1}{2}}^{1}\left(x^{2}+1\right) d x+\int_{1}^{2}(x+1) d x$
$=\left[\frac{x^{3}}{3}+x\right]_{\frac{1}{2}}^{1}+\left[\frac{x^{2}}{2}+x\right]_{1}^{2}$
$=\left[\frac{4}{3}-\frac{13}{24}\right]+\frac{5}{2}=\frac{79}{24}$
