The diameter of the circle, whose center lies on the line x+y=2 in the first quadrant and which touches both the lines x=3 and y=2, is
Question:
The diameter of the circle, whose centre lies on the line $x+y=2$ in the first quadrant and which touches both the lines $x=3$ and $y=2$, is____________
Solution:
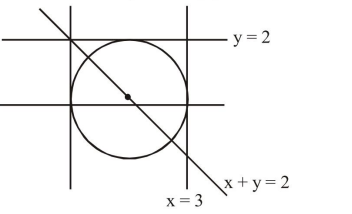
$\because \quad$ center lies on $x+y=2$ and in 1 st quadrant
center $=(\alpha, 2-\alpha)$
where $\alpha>0$ and $2-\alpha>0 \Rightarrow 0<\alpha<2$
$\because$ circle touches $x=3$ and $y=2$
$\Rightarrow|3-\alpha|=|2-(2-\alpha)|=$ radius
$\Rightarrow|3-\alpha|=|\alpha| \Rightarrow \alpha=\frac{3}{2}$
$\therefore \quad$ radius $=\alpha$
$\Rightarrow$ Diameter $=2 \alpha=3$
