The integral

$\int_{0}^{2}|x-1|-x \mid d x$

Let $f(x) \| x-1|-x|$

$= \begin{cases}1, & x \geq 1 \\ |1-2 x|, & x \leq 1\end{cases}$

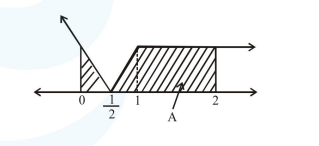
$A=\frac{1}{2}+1=\frac{3}{2}$

or

$\int_{0}^{1 / 2}(1-2 x) d x+\int_{1 / 2}^{1}(2 x-1)+\int_{0}^{2} 1 d x$

$=\left[x-x^{2}\right]_{0}^{1}+\left[x^{2}-x\right]_{1 / 2}^{1}+[x]_{1}^{2}$

$=3 / 2$