The locus of the midpoints of the chord of the circle,

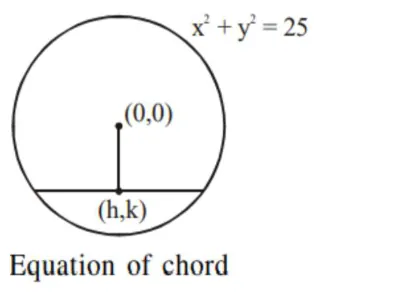
Equation of chord

$y-k=-\frac{h}{k}(x-h)$

$k y-k^{2}=-h x+h^{2}$

$h x+k y=h^{2}+k^{2}$

$y=-\frac{h x}{k}+\frac{h^{2}+k^{2}}{k}$

tangent to $\frac{x^{2}}{9}-\frac{y^{2}}{16}=1$

$c^{2}=a^{2} m^{2}-b^{2}$

$\left(\frac{h^{2}+k^{2}}{k}\right)^{2}=9\left(-\frac{h}{k}\right)^{2}-16$

$\left(x^{2}+y^{2}\right)^{2}=9 x^{2}-16 y^{2}$