Question.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.
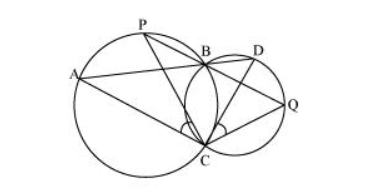

Solution:
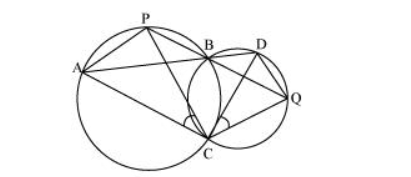
Join chords AP and DQ.
For chord AP,
$\angle P B A=\angle A C P$ (Angles in the same segment)...(1)
For chord DQ,
$\angle D B Q=\angle Q C D$ (Angles in the same segment) ... (2)
$A B D$ and $P B Q$ are line segments intersecting at $B$.
$\therefore \angle \mathrm{PBA}=\angle \mathrm{DBQ}($ Vertically opposite angles $) \ldots(3)$
From equations $(1),(2)$, and $(3)$, we obtain
$\angle A C P=\angle Q C D$

Join chords AP and DQ.
For chord AP,
$\angle P B A=\angle A C P$ (Angles in the same segment)...(1)
For chord DQ,
$\angle D B Q=\angle Q C D$ (Angles in the same segment) ... (2)
$A B D$ and $P B Q$ are line segments intersecting at $B$.
$\therefore \angle \mathrm{PBA}=\angle \mathrm{DBQ}($ Vertically opposite angles $) \ldots(3)$
From equations $(1),(2)$, and $(3)$, we obtain
$\angle A C P=\angle Q C D$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
