Two cubes have their volumes in the ratio 1 : 27.

The rate of the value of cubes = 1:27

$\frac{a_{1}^{3}}{a_{2}^{3}}=\frac{1}{27}$

$\frac{a_{1}}{a_{2}}=\frac{1}{3} \ldots \ldots(i)$

Now,

The ratio of their surface area

$s_{1}: s_{2}=6 a_{1}^{2}: 6 a_{2}^{2}$

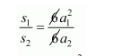
$=\left(\frac{a_{1}}{a_{2}}\right)^{2}$

$\frac{s_{1}}{s_{2}}=\frac{1}{9}$

Hence,

$s_{1}: s_{2}=1: 9$