Two electrons each are fixed at a distance '2d'.

Question:
Two electrons each are fixed at a distance '2d'. A third charge proton placed at the midpoint is displaced slightly by a distance $x(x<
$(\mathrm{m}=$ mass of charged particle $)$

(1) $\left(\frac{q^{2}}{2 \pi \varepsilon_{0} m d^{3}}\right)^{\frac{1}{2}}$
(2) $\left(\frac{\pi \varepsilon_{0} \mathrm{md}^{3}}{2 \mathrm{q}^{2}}\right)^{\frac{1}{2}}$
(3) $\left(\frac{2 \pi \varepsilon_{0} m d^{3}}{q^{2}}\right)^{\frac{1}{2}}$
(4) $\left(\frac{2 q^{2}}{\pi \varepsilon_{0} m d^{3}}\right)^{\frac{1}{2}}$

Correct Option: 1

Solution:

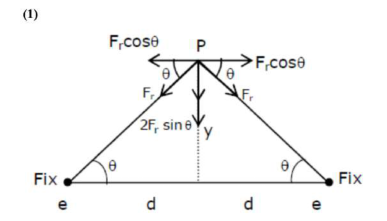
Restoring force on proton :-

$F_{r}=\frac{2 K q^{2} y}{\left[d^{2}+y^{2}\right]^{\frac{3}{2}}}$

$Y<<

$F_{r}=\frac{2 k q^{2} y}{d^{3}}=\frac{q^{2} y}{2 \pi \varepsilon_{0} d^{3}}=k y$

$\mathrm{K}=\frac{\mathrm{q}^{2}}{2 \pi \varepsilon_{0} \mathrm{~d}^{3}}$

Angular Frequency $: \omega=\sqrt{\frac{k}{m}}$

$\omega=\sqrt{\frac{q^{2}}{2 \pi \varepsilon_{0} m u^{3}}}$