Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide.

Solution:

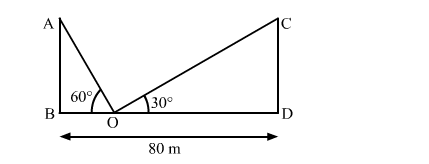
Let AB and CD be the equal poles; and BD be the width of the road.

We have,

$\angle \mathrm{AOB}=60^{\circ}$ and $\angle \mathrm{COD}=60^{\circ}$

In $\Delta \mathrm{AOB}$,

$\tan 60^{\circ}=\frac{\mathrm{AB}}{\mathrm{BO}}$

$\Rightarrow \sqrt{3}=\frac{\mathrm{AB}}{\mathrm{BO}}$

$\Rightarrow \mathrm{BO}=\frac{\mathrm{AB}}{\sqrt{3}}$

Also, in $\Delta \mathrm{COD}$,

$\tan 30^{\circ}=\frac{\mathrm{CD}}{\mathrm{DO}}$

$\Rightarrow \frac{1}{\sqrt{3}}=\frac{\mathrm{CD}}{\mathrm{DO}}$

$\Rightarrow \mathrm{DO}=\sqrt{3} \mathrm{CD}$

As, $B D=80$

$\Rightarrow \mathrm{BO}+\mathrm{DO}=80$

$\Rightarrow \frac{\mathrm{AB}}{\sqrt{3}}+\sqrt{3} \mathrm{CD}=80$

$\Rightarrow \frac{\mathrm{AB}}{\sqrt{3}}+\sqrt{3} \mathrm{AB}=80 \quad($ Given $: \mathrm{AB}=\mathrm{CD})$

$\Rightarrow \mathrm{AB}\left(\frac{1}{\sqrt{3}}+\sqrt{3}\right)=80$

$\Rightarrow \mathrm{AB}\left(\frac{1+3}{\sqrt{3}}\right)=80$

$\Rightarrow \mathrm{AB}\left(\frac{4}{\sqrt{3}}\right)=80$

$\Rightarrow \mathrm{AB}=\frac{80 \sqrt{3}}{4}$

$\Rightarrow \mathrm{AB}=20 \sqrt{3} \mathrm{~m}$

Also, $\mathrm{BO}=\frac{\mathrm{AB}}{\sqrt{3}}=\frac{20 \sqrt{3}}{\sqrt{3}}=20 \mathrm{~m}$

So, $\mathrm{DO}=80-20=60 \mathrm{~m}$

Hence, the height of each pole is $20 \sqrt{3} \mathrm{~m}$ and point $\mathrm{P}$ is at a distance of $20 \mathrm{~m}$ from left pole and $60 \mathrm{~m}$ from right pole.