Get important questions with answers of Ray Optics Class 12 for Boards exams. View the Physics Question Bank for Class 11 & 12 complete syllabus. These important questions will play significant role in clearing concepts of Physics. These questions with answers are designed keeping Ray Optics class 12 NCERT syllabus in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions with detailed solutions for ray optics class 12 Physics chapter. Learn all the important concepts of class 12 along with ray optics using these questions with their detailed answers.
Click Here for Detailed Chapter-wise Notes of PHYSICS for Class 12th, JEE & NEET. Hope you like these ray optics class 12 important questions with answers. With ray optics class 12 topic you can important questions with answers and notes of other topics of both classes(11 & 12). Q. When light of two colours A and B is passed through a plane boundary A is bent more than B.Which colour travels more slowly in the second medium
Ans. Since colour A is bent more towards the normal. Hence refractive index medium For colour A is more than that for colour B, As $v \propto \frac{1}{\mu},$ so colour A travels slowly in medium.
Q. An object is placed at the focus of concave lens. Where will its image be formed?
Ans. At a distance $\frac{f}{2}$ from the optical centre and on the same side of boject.
Q. A lens of glass is immersed in water. What will be its effect on the power of the lens?
Ans. Power of the lens increases
Q. A beam of light is converging towards a certain point. A parallel sided glass plate is introduced in the path of the converting beam. How will the point of convergence be shifted.
Ans. The point is
convergence will be shifted away from the glass plate. 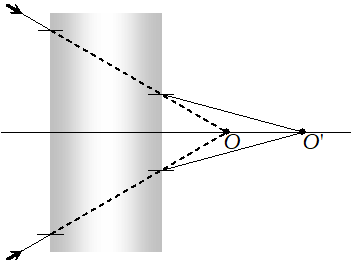
Q. A thin converging lens has a focal length ‘f’ in air. If it is complete immersed in a liquid, briefly explain how the focal length of the lens will vary?
Ans. According to lens makers formula $\frac{1}{f}=(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) \Rightarrow f \propto \frac{1}{(\mu-1)}$ As the refractive index of glass w.r.t. water is lesser than the refractive index of glass w.r.t. air, so focal length of converging lens will be more in water than that in air.
Q. What changes in the focal length of a (i) Concave mirror and (ii) convex lens occur, when the incident violet light on them is replaced with red light ?
Ans. (i) Focal length of concave mirror remains unchanged. (ii) For lens $\frac{1}{f} \propto(\mu-1)$ As $\mu_{V}>\mu_{R} \Rightarrow f_{R}>f_{V}$
Q. The image of a candle is formed by a convex lens on a screen. The lower half of the lens is painted black to make it completely opaque. Draw the ray diagram to show the image formation. How will this image be different from the one obtained when the lens is not painted black.
Ans. 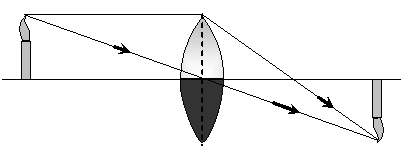
The image will still be of full size but the intensity of the image will be lesser, when the lower half of the lens in painted black.
Q. Give reasons for the following : (a) Rainbow is never observed on the surface of the Moon. (b) The Sun looks reddish at sunrise and sunset as viewed from Earth.
Ans. (a) There are no water vapours on the moon. Hence there is neither dispersion no total internal reflection of sun rays. Consequently, rainbow is never observed on the moon. (b) During sunrise on sunset, the sun is near the horizon. The shorter waves of blue region are scattered away by the greater thickness of the atmosphere. The least scattered red rays reach the observer. So the sun appears red.
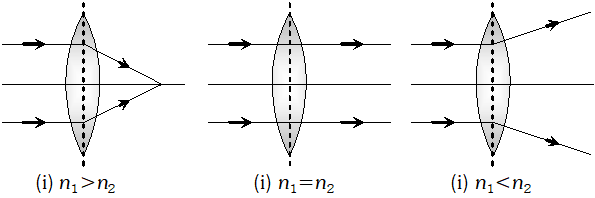
Q. A concave lens made of a material of refractive index $n_{1}$ is kept in a medium of refractive indexn $n_{2} .$ A parallel beam of light is incident on the lens.n Complete the path of rays of light emerging fromn the concave lens if ( i ) $n_{1}>n_{2}$ (ii) $n_{1}=n_{2}$ and (ini) $n_{1}
Ans. By using lens makers formula
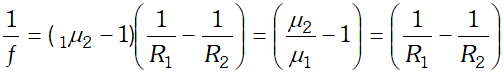
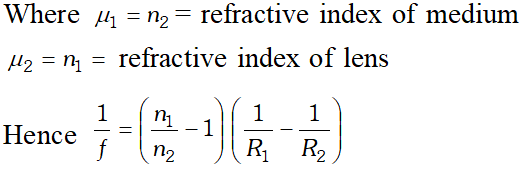
(i) If $n_{1}>n_{2}$ then $f$ will be positive. It means that lens will show opposite nature $i . e .$ it will converge the light rays (ii) If $n_{1}=n_{2}$ then $f$ will be infinite. It means that lens behaves like a plane glass plate i.e.n light raysn passes undeviated. (iii) If $n_{1}
Q. A convex lens made of a material of refractive index $n_{1}$ is kept in a medium of refractive index $n_{2}$. Parallel rays of light are incident on the lens. Complete the path of the rays of light emerging from the convex lens if $(\mathrm{i}) n_{1}>n_{2}$ (ii) $n_{1}=n_{2}$ and (iii) $n_{1}
Ans. By using lens makers formula $\quad \frac{1}{f}=\left(\frac{\mu_{2}}{\mu_{1}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ Where $\mu_{1}=n_{1}=$ refractive index of medium $\mu_{2}=n_{2}=$ refractive index of lens Hence $\frac{1}{f}=\left(\frac{n_{1}}{n_{2}}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ (i) If $n_{1}>n_{2}$ then $f$ will be positive. It means thatlens will show normal behaviour i.e. it will converge the light rays (ii) If $n_{1}=n_{2}$ then $f$ will be infinite. It means that lens behaves like a plane glass plate i.e. light rays passes undeviated (iii) If $n_{1}
Q. Draw the graph to show the variation of angle of deviation ‘D’ with the variation of angle of incidence ‘i’ for a monochromatic ray of light passing through a prism of refracting angle ‘A’. Deduce the relation$\mu=\frac{\sin \left[\frac{D_{m}+A}{2}\right]}{\frac{\sin A}{2}}$
Ans. 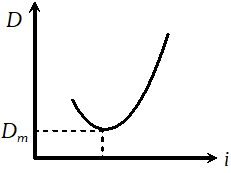
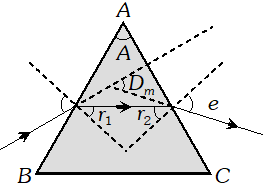
In the position of minimum deviation $i=e, r_{1}=r_{2}=r$ Hence by using $i+e=A+\delta \Rightarrow i+i=A+D_{m}$ $\Rightarrow i=\frac{A+D_{m}}{2}$ …(i) Also $A=r_{1}+r_{2}=r+r=2 r \Rightarrow r=\frac{A}{2}$ …(ii) Hence by using snell's $\operatorname{law} \mu=\frac{\sin i}{\sin r} \Rightarrow \mu=\frac{\sin \frac{A+D_{m}}{2}}{\sin A / 2}$
Q. The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose? [NCERT]
Ans. For a real image (on wall), minimum distance between the object and image should be $4 f .$ $\therefore 4 f=3 m \quad \therefore f=\frac{3}{4} m=0.75 m$
Q. Double convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of same radius of curvature. What is the radius of curvature required if focal length of lens is to be 20 cm. [NCERT]
Ans. Here, $\mu=1.55, R_{1}=R$ and $R_{2}=-R, f=20 \mathrm{cm}$ As $\frac{1}{f}=(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ $\therefore \frac{1}{20}=(1.55-1)\left(\frac{1}{R}+\frac{1}{R}\right)=\frac{1.10}{R}$$\Rightarrow \quad R=20 \times 1.1=22 \mathrm{cm}$
Q. A figure divide into squares, each of size 1 mm2 is being viewed at distance of 9 cm through a magnifying lens of focal length 10 cm, held close to the eye (a) Draw a ray diagram showing the formation of the image (b) What is the magnification produced by the lens? How much is the area of each square in the virtual image? (c) What is the angular magnification of the lens is to be 20 cm.? [NCERT]
Ans. (a)
Ray diagram 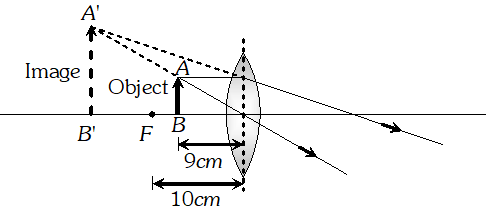
(b)
Magnification : Area of each square (i.e. object) $O=1 \mathrm{mm}^{2}$ Distance of object $u=-9 \mathrm{cm}$ Focal length of lens $f=+10 \mathrm{cm}$ By using lens formula $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$ $\frac{1}{10}=\frac{1}{v}-\frac{1}{(-9)} \Rightarrow \frac{1}{v}=\frac{1}{10}-\frac{1}{9}=-\frac{1}{90} \Rightarrow v=-90 \mathrm{cm}$ Hence magnification $=\frac{v}{u}=\frac{90}{9}=10$ also $m^{2}=\frac{A_{\text {image }}}{A_{\text {object }}} \Rightarrow A_{\text {image}}=m^{2} \times A_{\text {object}}$ $=(10)^{2} \times 1 m m^{2}=100 m m^{2}$ (c) Magnification power $=\frac{D}{4}=\frac{25}{9}=2.8=2.8$
Q. A converging lens has a focal length of 20 cm in air. It is made of material of refractive index 1.6. If it is immersed in a liquid of refractive 1.3, what will be its new focal length? How does the nature of the lens change if this lens is immersed in a liquid of refractive index 1.8 ?
Ans. By using lens makers formula
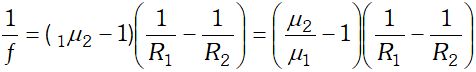
For the lens in air, $\mu_{2}=1.6, \mu_{1}=1,$ and $f=+20 \mathrm{cm}$
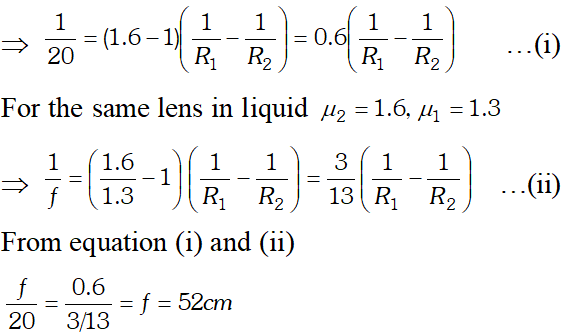
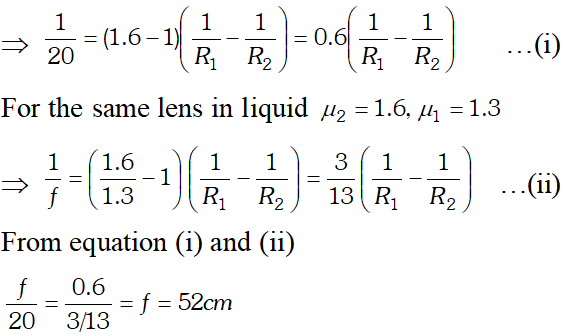
When lens is immersed in a liquid of $\mu=1.8$ then $\mu_{l e n s}<\mu_{m e d i u m} \mathrm{SO}$ lens behaves oppositely i.e like a diverging lens.
Q. A small candle 2.5 cm in size is placed 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to receive a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved? [NCERT]
Ans. Here, size of candle, $h_{1}=2.5 \mathrm{cm}, u=-27 \mathrm{cm}, R=-36 \mathrm{cm}$ $\quad f=\frac{R}{2}=-18 \mathrm{cm}, v=?,$ As $\frac{1}{u}+\frac{1}{v}=\frac{1}{f}$ $\therefore \frac{1}{v}=\frac{1}{f}-\frac{1}{u}=\frac{1}{-18}+\frac{1}{27}=\frac{-3+2}{54}=\frac{1}{54}$ or $v=-54 \mathrm{cm}$ $\therefore$ Screen should be placed at $54 \mathrm{cm}$ from the mirror on the same side as the object. If $h_{2}$ is size of image, then as the image is real $m=\frac{-h_{2}}{h_{1}}=\frac{-v}{-u}=\frac{v}{u} \Rightarrow \frac{-h_{2}}{2.5}=\frac{(-54)}{(-27)}=2$ $\Rightarrow h_{2}=-5 \mathrm{cm} .$ Minus sign indicates that image is inverted. When the candle is moved closer to mirror, the screen has to be moved away from the mirror. However, when candle is at a distance less than 18cm from the mirror, image formed would be virtual and screen is not required as image cannot be taken on the screen.
Q. An object of size 3 cm is placed 14 cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved farther from the lens ?
Ans. Here $h_{1}=3 c m, u=-14 c m, f=-21 c m, v=?$ As $\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$ $\frac{1}{v}=\frac{1}{f}+\frac{1}{u}=\frac{1}{-21}+\frac{1}{-14}=\frac{-5}{42} \Rightarrow v=\frac{-42}{5}=-8.4 \mathrm{cm}$ $\therefore$ Image is erect, virtual and at $8.4 \mathrm{cm}$ from the lens on the same side of the object. As $\frac{I}{O}=\frac{v}{u} \Rightarrow \frac{I}{3}=\frac{-8.4}{-14} \Rightarrow I=0.6 \times 3=1.8 \mathrm{cm}$ As the object is moved away from the lens, virtual image moves towards focus of lens (but never beyond focus). The size of image goes on decreasing.
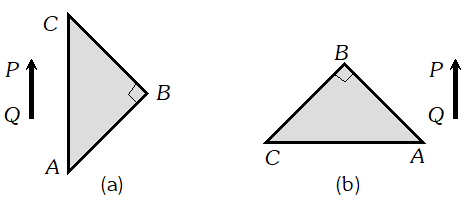
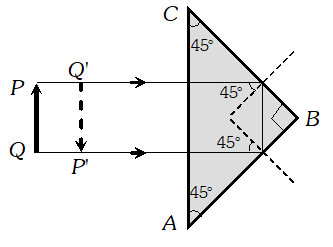
Q. Three light rays red (R), green (G) and blue (B) are incident on a right angled prism, ‘abc’ at face ‘ab’. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. Out of the three, which colour ray will emerge out of face ‘ac’? Justify your answer. Trace the path of green (G) ray after passing through face ‘ab’
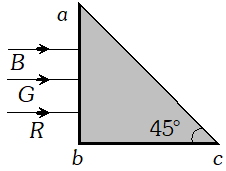
Ans. Since light rays incident normally on face ab, so no refraction takes place and light rays passes undeviated and then incident on face ac at an angle of $49^{\circ}$.
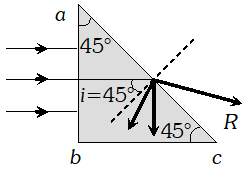
For total internal reflection at $a c$ $i>c \Rightarrow \sin i>\sin c \Rightarrow \sin 45^{\circ}>\frac{1}{\mu}$ $\Rightarrow \frac{1}{\sqrt{2}}>\frac{1}{\mu} \Rightarrow \mu>\sqrt{2}$ or $\mu>1.41$ As $\mu_{R}<\mu$ but $\mu_{G}>\mu$ and $\mu_{B}>\mu,$ so only red colour will be transmitted through face $a c$ while green and blue while internally reflected.
Q. A beam of light converges to a point P. A lens n placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20 cm. (b) a concave lens of focal length 16 cm.? Do the required calculations. [NCERT]
Ans. (a) For convex lens $u=+12 \mathrm{cm}, f=+20 \mathrm{cm}$ $\therefore \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \Rightarrow \frac{1}{20}=\frac{1}{v}-\frac{1}{12} \Rightarrow \frac{1}{20}+\frac{1}{12} \Rightarrow v=7.5 \mathrm{cm}$ Thus the beam converges at a point $7.5 \mathrm{cm}$ to the right of the lens.
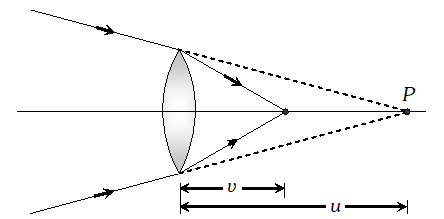 (b) For concave lens $u=+12 c m, f=-16 c m$ $\therefore \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \Rightarrow \frac{1}{-16}=\frac{1}{v}-\frac{1}{12} \Rightarrow \frac{1}{v}=\frac{-1}{16}+\frac{1}{12}$
(b) For concave lens $u=+12 c m, f=-16 c m$ $\therefore \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \Rightarrow \frac{1}{-16}=\frac{1}{v}-\frac{1}{12} \Rightarrow \frac{1}{v}=\frac{-1}{16}+\frac{1}{12}$ $\Rightarrow v=48 c m$ Thus the beam converges at a point 48 cm to the right of the lens.
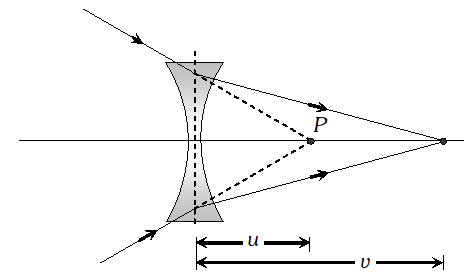
Q. Deduce lens maker’s formula for a thin bi-convex lens. Or Show by a diagram the image formation of a point object by a thin double convex lens having radii of curvature $R_{1}$ and $R_{2} .$ Hence derive the formula$\frac{1}{f}=(n-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) .$ Where $f$ is the focal length and n is refractive index of material of the lens.
Ans. A convex lens is made up of two convex spherical refracting surfaces. The final image is formed after two refractions. In figure (A) $P_{1}, P_{2}$ are the poles, of a thin biconvex lens with optical centre at $O$. Let $\mu_{2}$ be the refractive index of material of lens and $\mu_{1}$ be the refractive index of the surrounding.
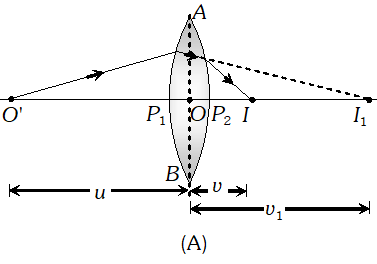
Consider a point object $O^{\prime}$ lying on the principle axis of the lens. The first refracting surface $A P_{1} B$ forms the image $I_{1}$ of the object at a distance $v_{1}$ from the surface. The image $I_{1}$ acts as a virtual object for the second surface that forms the final image at $I$. The general equation for refraction at spherical surface is
$\frac{\mu_{2}}{\text { distance of image }}-\frac{\mu_{1}}{\text { distance of object }}$ $=\frac{\mu_{2}-\mu_{1}}{\text { Radius of curvature }}$ …(i) To use this equation for the two surfaces $\left(A P_{1} B\right.$ and $\left.A P_{2} B\right)$ origin's are at $P_{1}$ and $P_{2}$ respectively. We should take the origin at O, because lens is Thin Refraction at first surface $A P_{1} B:$ For the first refraction object is at $O^{\prime}$ the image is at $I_{1}$ and centre of curvature of $C_{1}$. If $u, v_{1}$ and $R$ denotes their respective distance from $O$ then by using equation ( i ) $\frac{\mu_{2}}{v_{1}}-\frac{\mu_{1}}{u}=\frac{\mu_{2}-\mu_{2}}{R_{1}}$ …(ii)
Refraction at second surface $A P_{2} B:$ For the second refraction from surface $A P_{2} B, I_{1}$ acts as virtual object, $I$ is the final image and $C_{2}$ is the centre of curvature of this surface. If $v_{1}, v$ and $R_{2}$ denotes object distance, and image distance and radius of curvature for this surface then again by using equation ( i) $\frac{1 / \mu_{2}}{v}-\frac{1 / \mu_{1}}{v_{1}}=\frac{\mu_{2}-\mu_{2}}{R_{1}}$
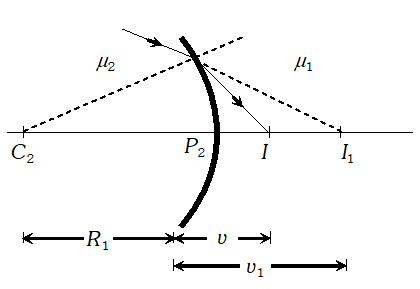
(Here $1 / \mu$ is taken in place of because refraction is taking place from denser to rarer medium)
$\Rightarrow \frac{\mu_{1}}{v}-\frac{\mu_{2}}{v_{1}}=\frac{\mu_{1}-\mu_{2}}{R_{2}}=-\frac{\left(\mu_{2}-\mu_{1}\right)}{R_{2}} \ldots$ (iii) on adding equation (ii) and (iii) we get $\frac{\mu_{1}}{v}-\frac{\mu_{1}}{u}=\mu_{2}-\mu_{1}\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ …(ii)
If $\mu_{1}=1$ and $\mu_{2}=\mu$ then $\frac{1}{f}=(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ this is the required result
Assumptions : (i) The lens is thin so that distances measured from the poles of it’s surface can be taken as equal to the distance from the optical centre of the lens (ii) The aperture of the lens is small. (iii) The object is point object (iv) The incident ray and refracted ray makes small angles with the principle axis of the lens.
Sign convention : (i) All distances are measured from the optical centre of the lens (ii) In the direction of light all the distances are taken positive while opposite to the direction of light all the distances are taken negative. (iii) Above the principal axis all the distances are taken positive while below the principal axis all distances are taken negative.
Click Here for Detailed Notes of any chapter.
Hope you like these ray optics classs 12 questions with answers. Along with ray optics you can get another tpics and chapters of class 12 and 11 notes along with these important questins with answers. eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc. We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one. Visit eSaral Website to download or view free study material for JEE & NEET. Also get to know about the strategies to Crack Exam in limited time period.

 (ii)
(ii) 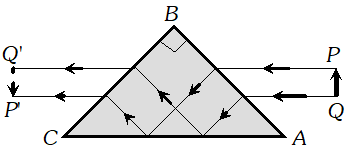
 The image will still be of full size but the intensity of the image will be lesser, when the lower half of the lens in painted black.
The image will still be of full size but the intensity of the image will be lesser, when the lower half of the lens in painted black. 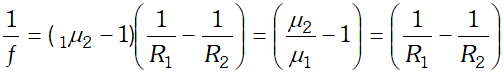
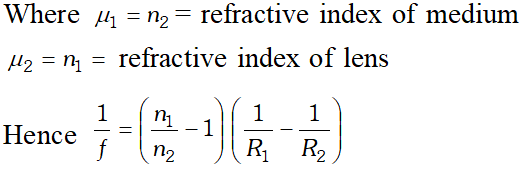 (i) If $n_{1}>n_{2}$ then $f$ will be positive. It means that lens will show opposite nature $i . e .$ it will converge the light rays (ii) If $n_{1}=n_{2}$ then $f$ will be infinite. It means that lens behaves like a plane glass plate i.e.n light raysn passes undeviated. (iii) If $n_{1}
(i) If $n_{1}>n_{2}$ then $f$ will be positive. It means that lens will show opposite nature $i . e .$ it will converge the light rays (ii) If $n_{1}=n_{2}$ then $f$ will be infinite. It means that lens behaves like a plane glass plate i.e.n light raysn passes undeviated. (iii) If $n_{1}

 In the position of minimum deviation $i=e, r_{1}=r_{2}=r$ Hence by using $i+e=A+\delta \Rightarrow i+i=A+D_{m}$ $\Rightarrow i=\frac{A+D_{m}}{2}$ …(i) Also $A=r_{1}+r_{2}=r+r=2 r \Rightarrow r=\frac{A}{2}$ …(ii) Hence by using snell's $\operatorname{law} \mu=\frac{\sin i}{\sin r} \Rightarrow \mu=\frac{\sin \frac{A+D_{m}}{2}}{\sin A / 2}$
In the position of minimum deviation $i=e, r_{1}=r_{2}=r$ Hence by using $i+e=A+\delta \Rightarrow i+i=A+D_{m}$ $\Rightarrow i=\frac{A+D_{m}}{2}$ …(i) Also $A=r_{1}+r_{2}=r+r=2 r \Rightarrow r=\frac{A}{2}$ …(ii) Hence by using snell's $\operatorname{law} \mu=\frac{\sin i}{\sin r} \Rightarrow \mu=\frac{\sin \frac{A+D_{m}}{2}}{\sin A / 2}$  (b) Magnification : Area of each square (i.e. object) $O=1 \mathrm{mm}^{2}$ Distance of object $u=-9 \mathrm{cm}$ Focal length of lens $f=+10 \mathrm{cm}$ By using lens formula $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$ $\frac{1}{10}=\frac{1}{v}-\frac{1}{(-9)} \Rightarrow \frac{1}{v}=\frac{1}{10}-\frac{1}{9}=-\frac{1}{90} \Rightarrow v=-90 \mathrm{cm}$ Hence magnification $=\frac{v}{u}=\frac{90}{9}=10$ also $m^{2}=\frac{A_{\text {image }}}{A_{\text {object }}} \Rightarrow A_{\text {image}}=m^{2} \times A_{\text {object}}$ $=(10)^{2} \times 1 m m^{2}=100 m m^{2}$ (c) Magnification power $=\frac{D}{4}=\frac{25}{9}=2.8=2.8$
(b) Magnification : Area of each square (i.e. object) $O=1 \mathrm{mm}^{2}$ Distance of object $u=-9 \mathrm{cm}$ Focal length of lens $f=+10 \mathrm{cm}$ By using lens formula $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$ $\frac{1}{10}=\frac{1}{v}-\frac{1}{(-9)} \Rightarrow \frac{1}{v}=\frac{1}{10}-\frac{1}{9}=-\frac{1}{90} \Rightarrow v=-90 \mathrm{cm}$ Hence magnification $=\frac{v}{u}=\frac{90}{9}=10$ also $m^{2}=\frac{A_{\text {image }}}{A_{\text {object }}} \Rightarrow A_{\text {image}}=m^{2} \times A_{\text {object}}$ $=(10)^{2} \times 1 m m^{2}=100 m m^{2}$ (c) Magnification power $=\frac{D}{4}=\frac{25}{9}=2.8=2.8$ ![]() For the lens in air, $\mu_{2}=1.6, \mu_{1}=1,$ and $f=+20 \mathrm{cm}$
For the lens in air, $\mu_{2}=1.6, \mu_{1}=1,$ and $f=+20 \mathrm{cm}$ 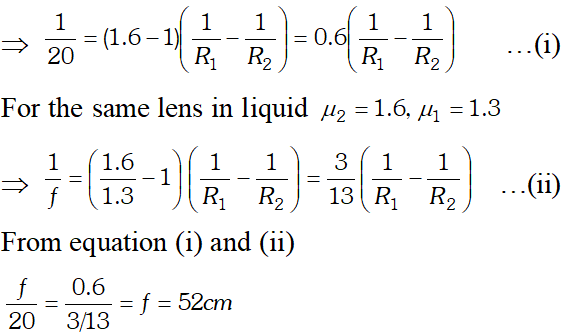
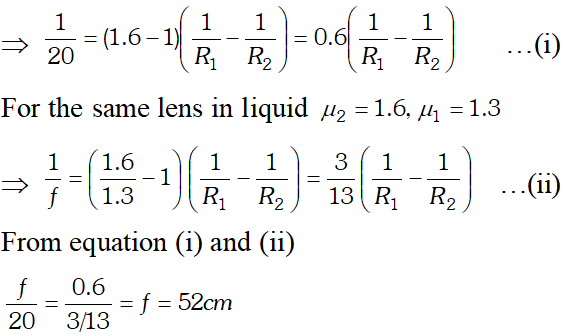

 For total internal reflection at $a c$ $i>c \Rightarrow \sin i>\sin c \Rightarrow \sin 45^{\circ}>\frac{1}{\mu}$ $\Rightarrow \frac{1}{\sqrt{2}}>\frac{1}{\mu} \Rightarrow \mu>\sqrt{2}$ or $\mu>1.41$ As $\mu_{R}<\mu$ but $\mu_{G}>\mu$ and $\mu_{B}>\mu,$ so only red colour will be transmitted through face $a c$ while green and blue while internally reflected.
For total internal reflection at $a c$ $i>c \Rightarrow \sin i>\sin c \Rightarrow \sin 45^{\circ}>\frac{1}{\mu}$ $\Rightarrow \frac{1}{\sqrt{2}}>\frac{1}{\mu} \Rightarrow \mu>\sqrt{2}$ or $\mu>1.41$ As $\mu_{R}<\mu$ but $\mu_{G}>\mu$ and $\mu_{B}>\mu,$ so only red colour will be transmitted through face $a c$ while green and blue while internally reflected.  (b) For concave lens $u=+12 c m, f=-16 c m$ $\therefore \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \Rightarrow \frac{1}{-16}=\frac{1}{v}-\frac{1}{12} \Rightarrow \frac{1}{v}=\frac{-1}{16}+\frac{1}{12}$ $\Rightarrow v=48 c m$ Thus the beam converges at a point 48 cm to the right of the lens.
(b) For concave lens $u=+12 c m, f=-16 c m$ $\therefore \frac{1}{f}=\frac{1}{v}-\frac{1}{u} \Rightarrow \frac{1}{-16}=\frac{1}{v}-\frac{1}{12} \Rightarrow \frac{1}{v}=\frac{-1}{16}+\frac{1}{12}$ $\Rightarrow v=48 c m$ Thus the beam converges at a point 48 cm to the right of the lens. 
 Consider a point object $O^{\prime}$ lying on the principle axis of the lens. The first refracting surface $A P_{1} B$ forms the image $I_{1}$ of the object at a distance $v_{1}$ from the surface. The image $I_{1}$ acts as a virtual object for the second surface that forms the final image at $I$. The general equation for refraction at spherical surface is $\frac{\mu_{2}}{\text { distance of image }}-\frac{\mu_{1}}{\text { distance of object }}$ $=\frac{\mu_{2}-\mu_{1}}{\text { Radius of curvature }}$ …(i) To use this equation for the two surfaces $\left(A P_{1} B\right.$ and $\left.A P_{2} B\right)$ origin's are at $P_{1}$ and $P_{2}$ respectively. We should take the origin at O, because lens is Thin Refraction at first surface $A P_{1} B:$ For the first refraction object is at $O^{\prime}$ the image is at $I_{1}$ and centre of curvature of $C_{1}$. If $u, v_{1}$ and $R$ denotes their respective distance from $O$ then by using equation ( i ) $\frac{\mu_{2}}{v_{1}}-\frac{\mu_{1}}{u}=\frac{\mu_{2}-\mu_{2}}{R_{1}}$ …(ii) Refraction at second surface $A P_{2} B:$ For the second refraction from surface $A P_{2} B, I_{1}$ acts as virtual object, $I$ is the final image and $C_{2}$ is the centre of curvature of this surface. If $v_{1}, v$ and $R_{2}$ denotes object distance, and image distance and radius of curvature for this surface then again by using equation ( i) $\frac{1 / \mu_{2}}{v}-\frac{1 / \mu_{1}}{v_{1}}=\frac{\mu_{2}-\mu_{2}}{R_{1}}$
Consider a point object $O^{\prime}$ lying on the principle axis of the lens. The first refracting surface $A P_{1} B$ forms the image $I_{1}$ of the object at a distance $v_{1}$ from the surface. The image $I_{1}$ acts as a virtual object for the second surface that forms the final image at $I$. The general equation for refraction at spherical surface is $\frac{\mu_{2}}{\text { distance of image }}-\frac{\mu_{1}}{\text { distance of object }}$ $=\frac{\mu_{2}-\mu_{1}}{\text { Radius of curvature }}$ …(i) To use this equation for the two surfaces $\left(A P_{1} B\right.$ and $\left.A P_{2} B\right)$ origin's are at $P_{1}$ and $P_{2}$ respectively. We should take the origin at O, because lens is Thin Refraction at first surface $A P_{1} B:$ For the first refraction object is at $O^{\prime}$ the image is at $I_{1}$ and centre of curvature of $C_{1}$. If $u, v_{1}$ and $R$ denotes their respective distance from $O$ then by using equation ( i ) $\frac{\mu_{2}}{v_{1}}-\frac{\mu_{1}}{u}=\frac{\mu_{2}-\mu_{2}}{R_{1}}$ …(ii) Refraction at second surface $A P_{2} B:$ For the second refraction from surface $A P_{2} B, I_{1}$ acts as virtual object, $I$ is the final image and $C_{2}$ is the centre of curvature of this surface. If $v_{1}, v$ and $R_{2}$ denotes object distance, and image distance and radius of curvature for this surface then again by using equation ( i) $\frac{1 / \mu_{2}}{v}-\frac{1 / \mu_{1}}{v_{1}}=\frac{\mu_{2}-\mu_{2}}{R_{1}}$  (Here $1 / \mu$ is taken in place of because refraction is taking place from denser to rarer medium) $\Rightarrow \frac{\mu_{1}}{v}-\frac{\mu_{2}}{v_{1}}=\frac{\mu_{1}-\mu_{2}}{R_{2}}=-\frac{\left(\mu_{2}-\mu_{1}\right)}{R_{2}} \ldots$ (iii) on adding equation (ii) and (iii) we get $\frac{\mu_{1}}{v}-\frac{\mu_{1}}{u}=\mu_{2}-\mu_{1}\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ …(ii) If $\mu_{1}=1$ and $\mu_{2}=\mu$ then $\frac{1}{f}=(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ this is the required result Assumptions : (i) The lens is thin so that distances measured from the poles of it’s surface can be taken as equal to the distance from the optical centre of the lens (ii) The aperture of the lens is small. (iii) The object is point object (iv) The incident ray and refracted ray makes small angles with the principle axis of the lens. Sign convention : (i) All distances are measured from the optical centre of the lens (ii) In the direction of light all the distances are taken positive while opposite to the direction of light all the distances are taken negative. (iii) Above the principal axis all the distances are taken positive while below the principal axis all distances are taken negative.
(Here $1 / \mu$ is taken in place of because refraction is taking place from denser to rarer medium) $\Rightarrow \frac{\mu_{1}}{v}-\frac{\mu_{2}}{v_{1}}=\frac{\mu_{1}-\mu_{2}}{R_{2}}=-\frac{\left(\mu_{2}-\mu_{1}\right)}{R_{2}} \ldots$ (iii) on adding equation (ii) and (iii) we get $\frac{\mu_{1}}{v}-\frac{\mu_{1}}{u}=\mu_{2}-\mu_{1}\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ …(ii) If $\mu_{1}=1$ and $\mu_{2}=\mu$ then $\frac{1}{f}=(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$ this is the required result Assumptions : (i) The lens is thin so that distances measured from the poles of it’s surface can be taken as equal to the distance from the optical centre of the lens (ii) The aperture of the lens is small. (iii) The object is point object (iv) The incident ray and refracted ray makes small angles with the principle axis of the lens. Sign convention : (i) All distances are measured from the optical centre of the lens (ii) In the direction of light all the distances are taken positive while opposite to the direction of light all the distances are taken negative. (iii) Above the principal axis all the distances are taken positive while below the principal axis all distances are taken negative. 