Here we will study about the Torque on a Bar Magnet in a Magnetic Field and Important Points related to it.
When a bar magnet is placed in a uniform magnetic field the two poles experience a force. The forces are equal in magnitude and opposite in direction and do not have same line of action. They constitute a couple of forces which produces a torque. The torque tries to rotate the magnet so as to align it parallel to direction of field.
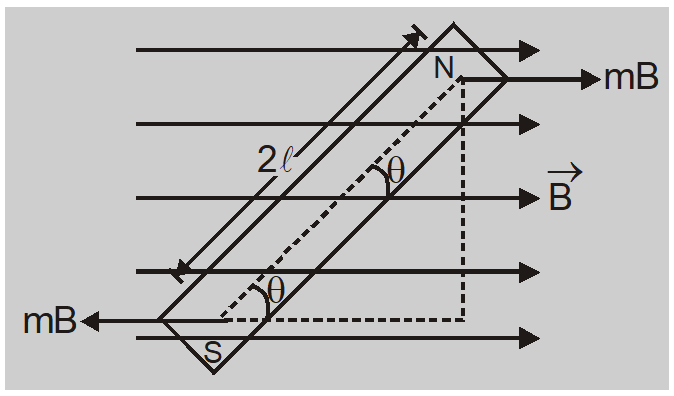Net force on bar magnet = $mB \hat{ i }+ mB (-\hat{ i })=0$
Torque $\tau=$ force $\times$ perpendicular distance between forces
$\tau= MB (2 \ell \sin \theta)= MB \sin \theta$
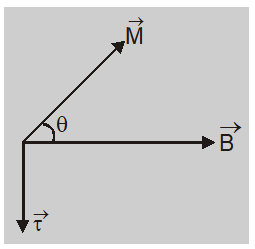In vector notation $\vec{\tau}=\vec{M} \times \vec{B}$
Important Points
Net force on bar magnet = $mB \hat{ i }+ mB (-\hat{ i })=0$
Torque $\tau=$ force $\times$ perpendicular distance between forces
$\tau= MB (2 \ell \sin \theta)= MB \sin \theta$
In vector notation $\vec{\tau}=\vec{M} \times \vec{B}$
Important Points
- When a bar magnet is kept in a uniform magnetic field it experiences no force.
- The bar magnet experiences a torque $\vec{\tau}=\vec{M} \times \vec{B}$ The direction of torque is perpendicular to plane containing $\overrightarrow{ M }$ and $\overrightarrow{ B }$. This torque produces rotational motion of magnet.
- $\tau=\tau_{\max }= mB$when $\theta=\frac{\pi}{2}$ The magnet experiences maximum torque when dipole moment vector is perpendicular to magnetic field.
- $\tau=\tau_{\min }=0$ when $\theta=0$ or $\pi$. The magnet experiences minimum torque when dipole moment vector is parallel or antiparalled to magnetic field.
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.For free video lectures and complete study material, Download eSaral APP.