True Dip and Apparent Dip - Magnetism and Matter Class 12

Here we will study about True Dip and Apparent Dip.

Apparent Dip

India's Best Exam Preparation for Class 12th - Download Now

The dip at a place is determined by a dip circle. It consists of a magnetized needle capable of rotation in a vertical plane about a horizontal axis. The needle moves over a vertical scale graduated in degrees.

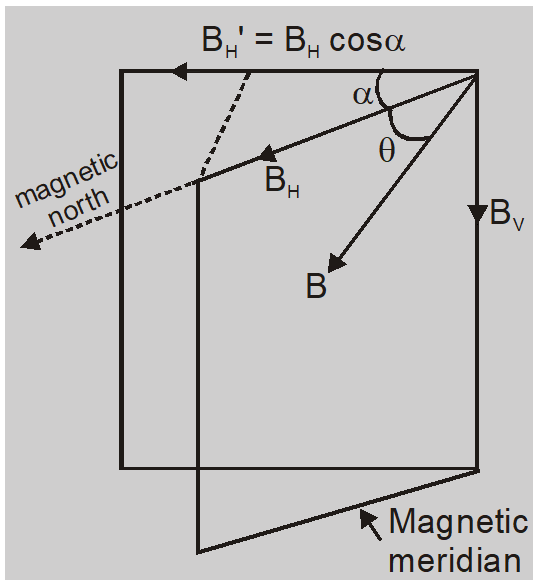
If the plane of the scale of the dip circle is not in the magnetic meridian then the needle will not indicate the correct direction of the earth's magnetic field. The angle made by the needle with the horizontal is called Apparent Dip.

India's Best Exam Preparation for Class 12th - Download Now

True Dip

When the plane of scale of the dip circle is in the magnetic meridian the needle comes to rest in direction of the earth's magnetic field. The angle made by the needle with the horizontal is called True Dip.

Suppose dip circle is set at angle $\alpha$ to the magnetic meridian.

Horizontal component $${B_H}' = {B_H}\cos \alpha $$

Vertical component ${B_V}' = {B_V}$ (remains unchanged)

Apparent dip is ${\theta ^\prime }\tan {\theta ^\prime } = {{{B_V}'} \over {{B_H}'}} = {{{B_V}} \over {{B_H}\cos \alpha }} = {{\tan \theta } \over {\cos \alpha }}\left( {\tan \theta = {{{B_V}} \over {{B_H}}} = {\rm{ true dip }}} \right)$

                                 

India's Best Exam Preparation for Class 12th - Download Now

1. For a vertical plane other than magnetic meridian $\alpha>0$ or $\cos \alpha<1$ so $\theta^{\prime}>\theta$ In a vertical plane other than magnetic meridian angle of dip is more than in magnetic meridian.
2. For a plane perpendicular to magnetic meridian $\alpha=\frac{\pi}{2}$ $\therefore \tan \theta^{\prime}=\infty \quad$ so $\quad \theta^{\prime}=\frac{\pi}{2}$ So in a plane perpendicular to magnetic meridian dip needle will become vertical.

At magnetic equator :

India's Best Exam Preparation for Class 12th - Download Now

1. The angle of dip is zero.
2. Vertical component of earths magnetic field becomes zero $B_{V}=B \sin \theta=B \sin 0=0$
3. A freely suspended magnet will become horizontal at the magnetic equator.
4. At the equator earth's magnetic field is parallel to the earth's surface i.e., horizontal.

At magnetic poles :

1. The angle of dip is $90^{\circ}$
2. Horizontal component of earth's magnetic field becomes zero. $B_{H}=B \cos \theta=B \cos 90=0$
3. A freely suspended magnet will become vertical at magnetic poles.
4. At poles, the earth's magnetic field is perpendicular to the surface of the earth i.e. vertical.

Ex. If $\theta_{1}$ and $\theta_{2}$ are angles of dip in two vertical planes at right angle to each other and $\theta$ is true dip then prove $\cot ^{2} \theta=\cot ^{2} \theta_{1}+\cot ^{2} \theta_{2}$.

Sol. If the vertical plane in which dip is $\theta_{1}$ subtends an angle $\alpha$ with meridian than other vertical plane in which dip is $\theta_{2}$ and is perpendicular to first will make an angle of $90-\alpha$ with magnetic meridian. If $\theta_{1}$ and $\theta_{2}$ are apparent dips than

$\tan \theta_{1}=\frac{B_{V}}{B_{H} \cos \alpha}$

$\tan \theta_{2}=\frac{B_{V}}{B_{H} \cos (90-\alpha)}=\frac{B_{V}}{B_{H} \sin \alpha}$

$\cot ^{2} \theta_{1}+\cot ^{2} \theta_{2}=\frac{1}{\left(\tan \theta_{1}\right)^{2}}+\frac{1}{\left(\tan \theta_{2}\right)^{2}}$

$=\frac{B_{H}^{2} \cos ^{2} \alpha+B_{H}^{2} \sin ^{2} \alpha}{B_{V}^{2}}=\frac{B_{H}^{2}}{B_{V}^{2}}$

$=\left(\frac{B \cos \theta}{B \sin \theta}\right)^{2}=\cot ^{2} \theta$

So $\quad \cot ^{2} \theta_{1}+\cot ^{2} \theta_{2}=\cot ^{2} \theta$

Also Read:
Properties of Paramagnetic & Diamagnetic Materials

India's Best Exam Preparation for Class 12th - Download Now

About eSaral

At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning

 personalized & adaptive for everyone.

India's Best Exam Preparation for Class 12th - Download Now

For free video lectures and complete study material, Download eSaral APP.