What is total internal reflection of light - Physics - eSaral

Hey, do you want to know What is a total internal reflection of light? If yes. Then you are at the right place.

Total internal Reflection

In case of refraction of light, from Snell’s law, we have

$\mu_{1} \sin \mathrm{i}=\mu_{2} \sin \mathrm{r}$......(1)

If the light is passing from denser to the rarer medium through a plane boundary then

$\mu_{1}=\mu_{\mathrm{D}}$

and

$\mu_{2}=\mu_{\mathrm{R}}$

so with $\mu=\left(\mu_{\mathrm{D}} / \mu_{\mathrm{R}}\right)$

$\sin \mathrm{i}=\frac{\mu_{\mathrm{R}}}{\mu_{\mathrm{D}}} \sin \mathrm{r}$

i.e. $\sin \mathrm{i}=\frac{\sin \mathrm{r}}{\mu}$.....(2)

i.e.$\sin \mathrm{i} \alpha \sin \mathrm{r}$

with $(\angle \mathrm{i})<(\angle \mathrm{r})($ as $\mu>1)$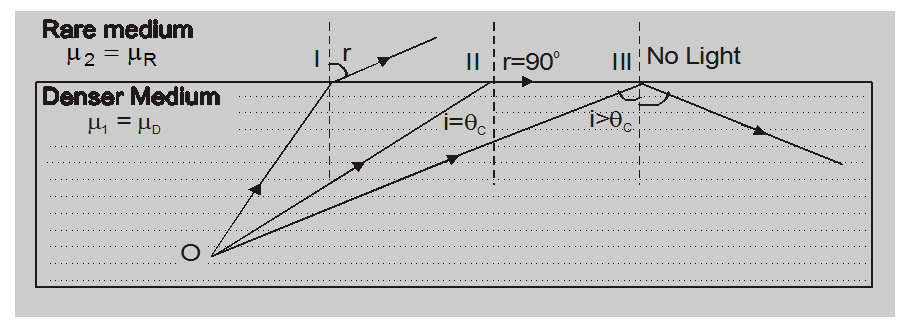


So as the angle of the incident I increase the angle of refraction r will also increase and for a certain value of i $\left(\angle 90^{\circ}\right)$ r will become $90^{\circ}$. The value of angle of incidence for which $r=90^{\circ}$ is called critical angle and is denoted by $\theta_{\mathrm{c}}$. From eq. (2)

$\sin \theta_{C}=\frac{\sin 90}{\mu}$

i.e., $\sin \theta_{\mathrm{C}}=\frac{1}{\mu}$.....(3)

And hence eqn. (2) in terms of critical angle can be written as

$\sin \mathrm{i}=\sin \mathrm{r} \mathrm{X} \sin \theta_{\mathrm{c}}$

$\sin r=\frac{\sin i}{\sin \theta_{c}}$.....(4)

So if $i>\theta_{c} \sin r>1$. This means that r is imaginary (as the value of sin of any angle can never be greater than unit) physically this situation implies that refracted ray does not exist. So, the total light incident of the boundary will be reflected back into the same medium from the boundary. This phenomenon is called total internal reflection.

Special Note:

1. For total internal reflection to take place light from air to water (or glass) and from water to glass total internal reflection can-never take place.
   
   
2. When light is passing from denser to rare medium total internal reflection will take place only if the angle of incidence is greater than a certain value called critical angle given by
   
   $\theta_{\mathrm{C}}=\sin ^{-1}\left[\frac{1}{\mu}\right]$
   
   with
   
   $\mu=\frac{\mu_{\mathrm{D}}}{\mu_{\mathrm{R}}}$
   
   
3. In the case of total internal reflection as all (i.e. 100%) incident light is reflected back into the same medium there is no loss of intensity while in the case of reflection from mirror or refraction from lenses there is some loss of intensity as all light can never be reflected or refracted. This is why image formed by TIR is much bright than formed by mirror or lenses.

Critical angle ($\theta_{\mathrm{c}}$)

In case of propagation of light from denser of rate medium through a plane boundary, the critical angle is the angle of incidence for which angle of refraction is $90^{\circ}$ and so from Snell’s law

$\mu \sin i=\mu_{2} \sin r$

$\mu_{\mathrm{D}} \sin \theta_{\mathrm{C}}=\mu_{\mathrm{R}} \sin 90$

$\sin \theta_{\mathrm{C}}=\frac{\mu_{\mathrm{R}}}{\mu_{\mathrm{D}}}=\left[\frac{1}{\mu}\right]$

with $\mu=\frac{\mu_{\mathrm{D}}}{\mu_{\mathrm{R}}}$

or $\theta_{C}=\sin ^{-1}\left(\frac{1}{\mu}\right)$

1. For a given pair of medium critical angle depends on wavelength of light used i.e., greater the wavelength of light lesser will be $\mu$ $\left[\right.$ as a $\left.\mu \alpha \frac{1}{v} \alpha \frac{1}{\lambda}\right]$
   
   and so greater will be the critical angle. This is why the critical angle is maximum for red and minimum for violet rays.

For a given light is depends on the nature of the pair of medium lesser the greater will the critical angle and vice–versa. This is why in the case of



Some illustration of total internal reflection:

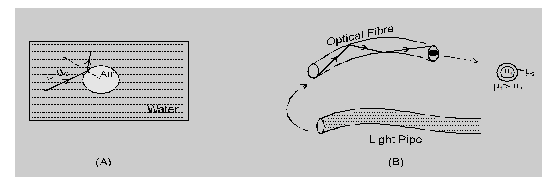
1. Shining of air bubble
2. Sparking of diamond
3. Optical – fiber
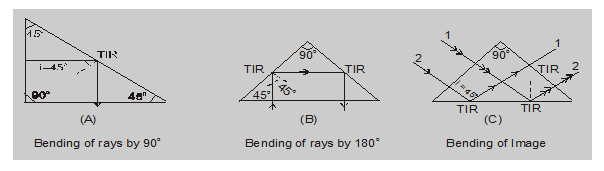
4. Action of 'Porro' prism
5. Duration of suns visibility
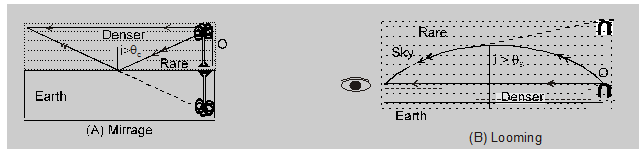
6. Mirrage and looming

So, that's all from this article. I hope you get the idea about What is a total internal reflection of light. If you found this article informative then please share it with your friends. If you have any confusion related to this topic then you can ask in the comments section down below.

For a better understanding of this chapter, please check the detailed notes of Ray Optics class 12 . To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.