Do you know about the Ampere's Circuital Law, well it is a current distribution that helps us to calculate the magnetic field, And yes, Biot-Savart's law does the same but Ampere’s law uses the case high symmetry. We will first understand the ampere’s circuital law, its definition, formulae, & Applications of Ampere's Law in detail,
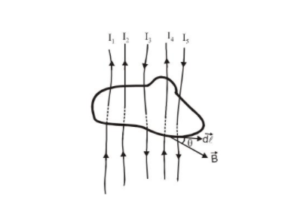
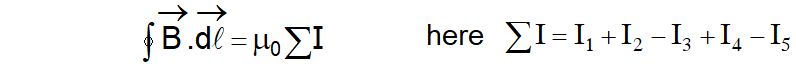
This result is independent of the size and shape of the closed curve enclosing a current.
This is known as Ampere's circuital law.
Ampere's law gives another method to calculate the magnetic field due to a given current distribution.
Ampere's law may be derived from the Biot-Savart law and Biot-Savart law may be derived from the Ampere's law.
Ampere's law is more useful under certain symmetrical conditions.
Biot-Savart law based on the experimental results whereas Ampere's law based on mathematical.
Consider a close circular loop as shown in the figure.
 According to Ampere's law $\oint \overrightarrow{\mathrm{B}} . \overrightarrow{\mathrm{d}} \ell=\mu_{0} \sum \mathrm{I}$
According to Ampere's law $\oint \overrightarrow{\mathrm{B}} . \overrightarrow{\mathrm{d}} \ell=\mu_{0} \sum \mathrm{I}$
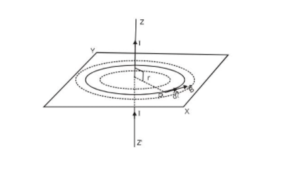
The direction of $\overrightarrow{\mathrm{B}}$ at every point is along the tangent to the circle.
Consider a small element $\overrightarrow{\mathrm{d} \ell}$ of the circle of radius r at P. The direction of $\overrightarrow{\mathrm{B}}$ and $\overrightarrow{\mathrm{d} \ell}$ the same. Therefore, angle between them is zero.
Line integral of $\overrightarrow{\mathrm{B}}$ around the complete circular path of radius $\mathrm{r}$ is given by
 $\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} \ell=\oint \mathrm{B} \mathrm{d} \ell \cos 0^{\circ}$ $=\quad \mathrm{B} \oint \mathrm{d} \ell=\mathrm{B} \times 2 \pi \mathrm{r}$ $(\oint \mathrm{d} \ell=2 \pi \mathrm{r}=$ cicumference of the circle.) and $\quad \sum I=I$
$\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} \ell=\oint \mathrm{B} \mathrm{d} \ell \cos 0^{\circ}$ $=\quad \mathrm{B} \oint \mathrm{d} \ell=\mathrm{B} \times 2 \pi \mathrm{r}$ $(\oint \mathrm{d} \ell=2 \pi \mathrm{r}=$ cicumference of the circle.) and $\quad \sum I=I$
So we get $\mathrm{B} \times 2 \pi \mathrm{r}=\mu_{0} \mathrm{I}$
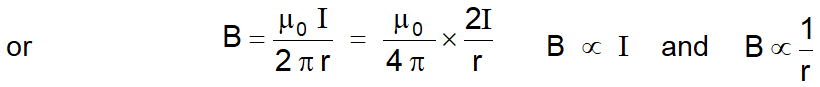
For finding the behavior of magnetic field due to this wire, let us divide the whole region into two parts.
(a) $\mathrm{r} \geq \mathrm{R}$ and
(b) $\mathrm{r}<\mathrm{R}$
$r=$ distance from the centre of the wire.
For $\mathrm{r} \geq \mathrm{R}:$ For closed circular path denoted by ( 1) from symmetry $\overrightarrow{\mathrm{B}}$ must be constant in magnitude and parallel to $\overrightarrow{\mathrm{d} \ell}$ at every point on this circle. Because the total current passing through the plane of the circle is I.
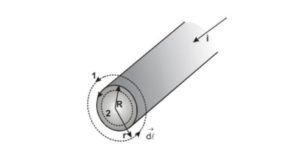
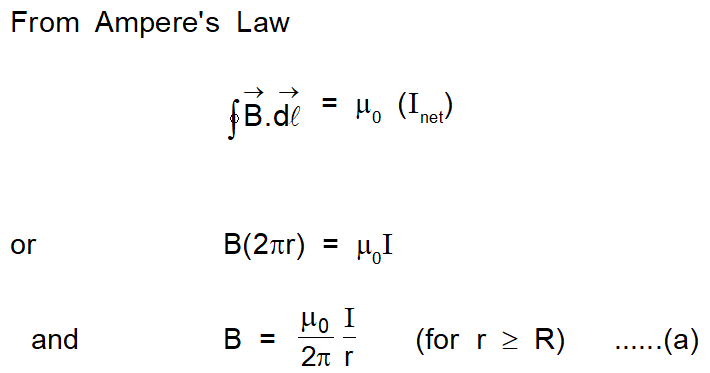
For $\mathrm{r}<\mathrm{R}:$ The current $\mathrm{I}$ passing through the plane of circle 2 is less than the total current I. Because the current is uniform over the cross-section of the wire.
Current through unit area $=\frac{\mathrm{I}}{\pi \mathrm{R}^{2}}$
So current through area enclosed by circle 2 is $\mathrm{I}^{\prime}=\frac{\mathrm{I} \pi \mathrm{r}^{2}}{\pi \mathrm{R}^{2}}$
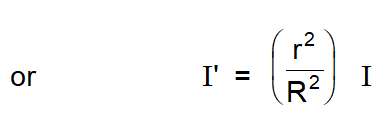
Now we apply Ampere's law for circle $2 .$
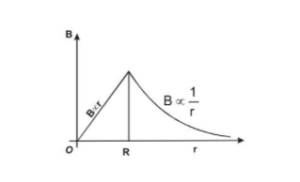
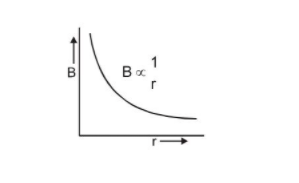
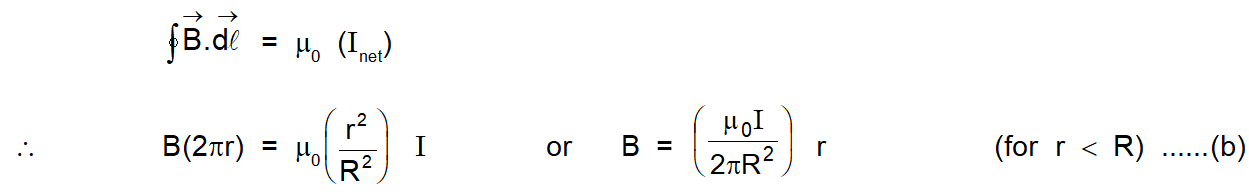 The magnitude of the magnetic field versus $r$ for this configuration is plotted in figure. Note that inside the wire $\mathrm{B} \rightarrow 0$ as $\mathrm{r} \rightarrow 0 .$ Note also that eqn. (a) and eqn (b) give the same value of the magnetic field at $r=R,$ demonstrating that the magnetic field is continuous at the surface of the wire.
The magnitude of the magnetic field versus $r$ for this configuration is plotted in figure. Note that inside the wire $\mathrm{B} \rightarrow 0$ as $\mathrm{r} \rightarrow 0 .$ Note also that eqn. (a) and eqn (b) give the same value of the magnetic field at $r=R,$ demonstrating that the magnetic field is continuous at the surface of the wire.
 (I) $\quad$ For $r
(I) $\quad$ For $r
$\sum \mathrm{I}=0$ and hence $\quad B=0$
(II) $\quad$ For $r_{1}
Now current I is flowing through area $\left[\pi r_{2}^{2}-\pi r_{1}^{2}\right]$
So, current per unit area $=\frac{I}{\pi\left(r_{2}^{2}-r_{1}^{2}\right)}$
$\therefore$ current flowing through area in bet" $\mathrm{r}_{1}<\mathrm{r}<\mathrm{r}_{2}$ is $\mathrm{I}=\frac{\mathrm{I}}{\pi\left(\mathrm{r}_{2}^{2}-\mathrm{r}_{1}^{2}\right)} \times\left(\pi \mathrm{r}^{2}-\pi \mathrm{r}_{1}^{2}\right)$
by using ampere's law for circle of radius $\mathrm{r} \oint \overrightarrow{\mathrm{B}} . \overrightarrow{\mathrm{d}} \vec{\ell}=\mu_{0} \sum \mathrm{I}$
or $\quad \oint B d \ell \cos 0^{\circ}=\mu_{0}\left[\frac{I\left(r^{2}-r_{1}^{2}\right)}{r_{2}^{2}-r_{1}^{2}}\right]$
or $\quad \mathrm{B} \oint \mathrm{d} \ell=\mu_{0} \mathrm{I}\left[\frac{\mathrm{r}^{2}-\mathrm{r}_{1}^{2}}{\mathrm{r}_{2}^{2}-\mathrm{r}_{1}^{2}}\right]$
or $\quad B=\frac{\mu_{0} I}{2 \pi r}\left[\frac{r^{2}-r_{1}^{2}}{r_{1}^{2}-r_{1}^{2}}\right]$
$[\because \oint \mathrm{d} \ell=2 \pi \mathrm{r}]$
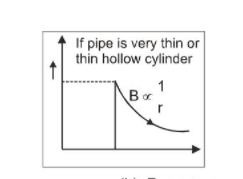
(a) For $r=r_{2}$
$B=\frac{\mu_{0} I}{2 \pi r_{2}}$
(b) For $r>r_{2}$
$B=\frac{\mu_{0} I}{2 \pi r}$
Also Read: Biot Savart's Law Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.
For free video lectures and complete study material, Download eSaral APP.
- Magnetic induction due to a long current-carrying wire.
- The Magnetic field created by a long current carrying conducting cylinder
- Magnetic field due to a conducting current-carrying hollow cylinder
Ampere's Circuital Law
Ampere's circuital law states that the line integral of magnetic field induction $\overrightarrow{\mathrm{B}}$ around any closed path in a vacuum is equal to $\mu_{0}$ times the total current threading the closed path, i.e.,
This result is independent of the size and shape of the closed curve enclosing a current.
This is known as Ampere's circuital law.
Ampere's law gives another method to calculate the magnetic field due to a given current distribution.
Ampere's law may be derived from the Biot-Savart law and Biot-Savart law may be derived from the Ampere's law.
Ampere's law is more useful under certain symmetrical conditions.
Biot-Savart law based on the experimental results whereas Ampere's law based on mathematical.
Applications of Ampere's Law
(a) Magnetic induction due to a long current-carrying wire.
Consider a long straight conductor Z-Z' is along the z-axis. Let I will be the current flowing in the direction as shown in Fig. The magnetic field is produced around the conductor. The magnetic lines of force are concentric circles in the XY plane as shown by dotted lines. Let the magnitude of the magnetic field induction produced at a point P at distance r from the conductor isConsider a close circular loop as shown in the figure.
 According to Ampere's law $\oint \overrightarrow{\mathrm{B}} . \overrightarrow{\mathrm{d}} \ell=\mu_{0} \sum \mathrm{I}$
According to Ampere's law $\oint \overrightarrow{\mathrm{B}} . \overrightarrow{\mathrm{d}} \ell=\mu_{0} \sum \mathrm{I}$
The direction of $\overrightarrow{\mathrm{B}}$ at every point is along the tangent to the circle.
Consider a small element $\overrightarrow{\mathrm{d} \ell}$ of the circle of radius r at P. The direction of $\overrightarrow{\mathrm{B}}$ and $\overrightarrow{\mathrm{d} \ell}$ the same. Therefore, angle between them is zero.
Line integral of $\overrightarrow{\mathrm{B}}$ around the complete circular path of radius $\mathrm{r}$ is given by
 $\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} \ell=\oint \mathrm{B} \mathrm{d} \ell \cos 0^{\circ}$ $=\quad \mathrm{B} \oint \mathrm{d} \ell=\mathrm{B} \times 2 \pi \mathrm{r}$ $(\oint \mathrm{d} \ell=2 \pi \mathrm{r}=$ cicumference of the circle.) and $\quad \sum I=I$
$\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d}} \ell=\oint \mathrm{B} \mathrm{d} \ell \cos 0^{\circ}$ $=\quad \mathrm{B} \oint \mathrm{d} \ell=\mathrm{B} \times 2 \pi \mathrm{r}$ $(\oint \mathrm{d} \ell=2 \pi \mathrm{r}=$ cicumference of the circle.) and $\quad \sum I=I$
So we get $\mathrm{B} \times 2 \pi \mathrm{r}=\mu_{0} \mathrm{I}$
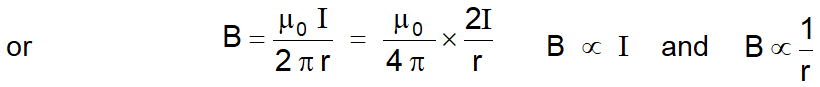
(b) Magnetic field created by a long current carrying conducting cylinder
A long straight wire of radius R carries a steady current I that is uniformly distributed through the cross-section of the wire.For finding the behavior of magnetic field due to this wire, let us divide the whole region into two parts.
(a) $\mathrm{r} \geq \mathrm{R}$ and
(b) $\mathrm{r}<\mathrm{R}$
$r=$ distance from the centre of the wire.
For $\mathrm{r} \geq \mathrm{R}:$ For closed circular path denoted by ( 1) from symmetry $\overrightarrow{\mathrm{B}}$ must be constant in magnitude and parallel to $\overrightarrow{\mathrm{d} \ell}$ at every point on this circle. Because the total current passing through the plane of the circle is I.

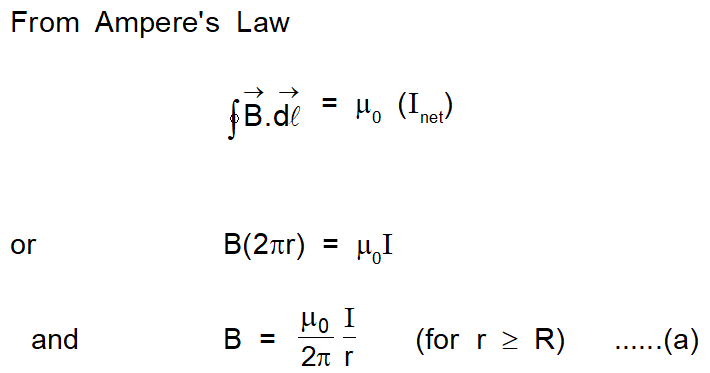
For $\mathrm{r}<\mathrm{R}:$ The current $\mathrm{I}$ passing through the plane of circle 2 is less than the total current I. Because the current is uniform over the cross-section of the wire.
Current through unit area $=\frac{\mathrm{I}}{\pi \mathrm{R}^{2}}$
So current through area enclosed by circle 2 is $\mathrm{I}^{\prime}=\frac{\mathrm{I} \pi \mathrm{r}^{2}}{\pi \mathrm{R}^{2}}$
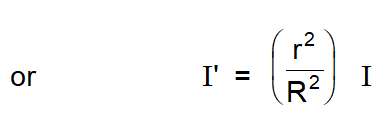
Now we apply Ampere's law for circle $2 .$

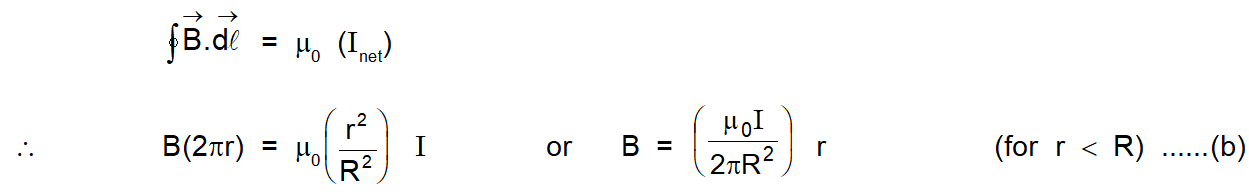 The magnitude of the magnetic field versus $r$ for this configuration is plotted in figure. Note that inside the wire $\mathrm{B} \rightarrow 0$ as $\mathrm{r} \rightarrow 0 .$ Note also that eqn. (a) and eqn (b) give the same value of the magnetic field at $r=R,$ demonstrating that the magnetic field is continuous at the surface of the wire.
The magnitude of the magnetic field versus $r$ for this configuration is plotted in figure. Note that inside the wire $\mathrm{B} \rightarrow 0$ as $\mathrm{r} \rightarrow 0 .$ Note also that eqn. (a) and eqn (b) give the same value of the magnetic field at $r=R,$ demonstrating that the magnetic field is continuous at the surface of the wire.
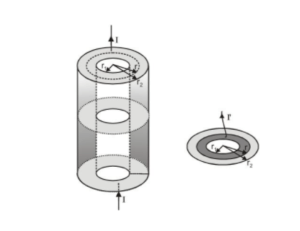
(c) Magnetic field due to a conducting current carrying hollow cylinder
Consider a conducting hollow cylinder with inner radius $r_{1}$ and outer radius $r_{2} .$ And current $\mathrm{I}$ is flowing through it. (I) $\quad$ For $r
(I) $\quad$ For $r$\sum \mathrm{I}=0$ and hence $\quad B=0$
(II) $\quad$ For $r_{1}
Now current I is flowing through area $\left[\pi r_{2}^{2}-\pi r_{1}^{2}\right]$
So, current per unit area $=\frac{I}{\pi\left(r_{2}^{2}-r_{1}^{2}\right)}$
$\therefore$ current flowing through area in bet" $\mathrm{r}_{1}<\mathrm{r}<\mathrm{r}_{2}$ is $\mathrm{I}=\frac{\mathrm{I}}{\pi\left(\mathrm{r}_{2}^{2}-\mathrm{r}_{1}^{2}\right)} \times\left(\pi \mathrm{r}^{2}-\pi \mathrm{r}_{1}^{2}\right)$
by using ampere's law for circle of radius $\mathrm{r} \oint \overrightarrow{\mathrm{B}} . \overrightarrow{\mathrm{d}} \vec{\ell}=\mu_{0} \sum \mathrm{I}$
or $\quad \oint B d \ell \cos 0^{\circ}=\mu_{0}\left[\frac{I\left(r^{2}-r_{1}^{2}\right)}{r_{2}^{2}-r_{1}^{2}}\right]$
or $\quad \mathrm{B} \oint \mathrm{d} \ell=\mu_{0} \mathrm{I}\left[\frac{\mathrm{r}^{2}-\mathrm{r}_{1}^{2}}{\mathrm{r}_{2}^{2}-\mathrm{r}_{1}^{2}}\right]$
or $\quad B=\frac{\mu_{0} I}{2 \pi r}\left[\frac{r^{2}-r_{1}^{2}}{r_{1}^{2}-r_{1}^{2}}\right]$
$[\because \oint \mathrm{d} \ell=2 \pi \mathrm{r}]$

(a) For $r=r_{2}$
$B=\frac{\mu_{0} I}{2 \pi r_{2}}$
(b) For $r>r_{2}$
$B=\frac{\mu_{0} I}{2 \pi r}$
Also Read: Biot Savart's Law Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.
For free video lectures and complete study material, Download eSaral APP.
Comments
Yasir Ayoub
March 2, 2021, 9:10 p.m.
Application of ampere circuital law to find magnetic intensity due to long cylindrical wire,due to a long solenoid
