Here are the Conservation of angular momentum examples:
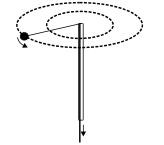 (i) A point mass is tied to one end of a cord whose other end passes through a vertical hollow tube, caught in one hand. The point mass is being rotated in a horizontal circle. The cord is then pulled down so that the radius of the circle reduces.
Here the force on the point mass due to cord is radial and hence the torque about the center of rotation is zero therefore, the angular momentum must remain constant as the cord shortend.
As cord is pulled down, the point mass rotates faster than before. The reason is that by shortening the radius of the circle, the moment of inertia of point mass about axis of rotation decreases
$\mathrm{I}_{\mathrm{i}} \omega_{\mathrm{i}}=\mathrm{I}_{\mathrm{f}} \omega_{\mathrm{f}} \quad \mathrm{I}_{\mathrm{i}}>\mathrm{I}_{\mathrm{f}} \quad$ so $\omega_{\mathrm{i}}<\omega_{\mathrm{f}}$
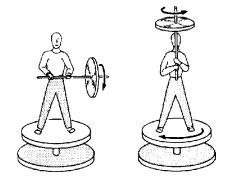
(ii) A man with his arms outstretched and holding heavy bells in each
hand, is standing at the centre of a rotating table. When the man pulls his arms,
the speed of rotation of the table increases. The reason is that on pulling the
(i) A point mass is tied to one end of a cord whose other end passes through a vertical hollow tube, caught in one hand. The point mass is being rotated in a horizontal circle. The cord is then pulled down so that the radius of the circle reduces.
Here the force on the point mass due to cord is radial and hence the torque about the center of rotation is zero therefore, the angular momentum must remain constant as the cord shortend.
As cord is pulled down, the point mass rotates faster than before. The reason is that by shortening the radius of the circle, the moment of inertia of point mass about axis of rotation decreases
$\mathrm{I}_{\mathrm{i}} \omega_{\mathrm{i}}=\mathrm{I}_{\mathrm{f}} \omega_{\mathrm{f}} \quad \mathrm{I}_{\mathrm{i}}>\mathrm{I}_{\mathrm{f}} \quad$ so $\omega_{\mathrm{i}}<\omega_{\mathrm{f}}$
(ii) A man with his arms outstretched and holding heavy bells in each
hand, is standing at the centre of a rotating table. When the man pulls his arms,
the speed of rotation of the table increases. The reason is that on pulling the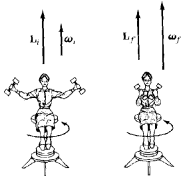 arms, the distance R of the dumbells from the axis of rotation decreases and so the moment of inertia decreases. Therefore, by conservation of angular momentum, the angular velocity increases.
arms, the distance R of the dumbells from the axis of rotation decreases and so the moment of inertia decreases. Therefore, by conservation of angular momentum, the angular velocity increases.
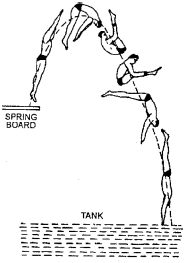 (iii) When a diver jumps into water from a height, he does not keep his body straight but pulls in his arms and legs towards the centre of his body. On doing so, the moment of inertia I of his body decreases. But since the angular momentum I $\omega$ remains constant, his angular velocity $\omega$ correspondingly increases.
Hence during jumping he can rotate his body in the air.
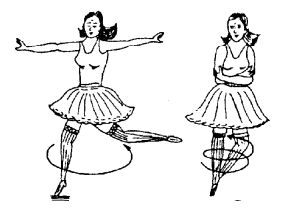
(iv) In the same way, the ice skater and the ballet dancer increase or decrease the angular velocity of spin about a vertical axis by pulling or
extending out their limbs.
(iii) When a diver jumps into water from a height, he does not keep his body straight but pulls in his arms and legs towards the centre of his body. On doing so, the moment of inertia I of his body decreases. But since the angular momentum I $\omega$ remains constant, his angular velocity $\omega$ correspondingly increases.
Hence during jumping he can rotate his body in the air.
(iv) In the same way, the ice skater and the ballet dancer increase or decrease the angular velocity of spin about a vertical axis by pulling or
extending out their limbs.
 (v) A: axis is horizontal; angular momentum about vertical axis $=0$. B: axis is vertical; angular momentum about vertical axis is still zero; man and chair spin in direction opposite to spin of the wheel.
(v) A: axis is horizontal; angular momentum about vertical axis $=0$. B: axis is vertical; angular momentum about vertical axis is still zero; man and chair spin in direction opposite to spin of the wheel.
 (vi) The angular velocity of a planet around the Sun increases when it comes near the Sun. When a planet revolving around the Sun in an elliptical orbit comes near the Sun, the moment of inertia of the planet about the Sun decreases. In order to conserve angular momentum, the angular velocity shall increase. Similarly, when the planet is away from the Sun, there will be a decreases in the angular velocity.
(vii) The speed of the inner layers of the whirlwind in a tornado is alarmingly high, In a tornado, the moment of inertia of air will go on decreasing as the air moves the centre. This will be accompanied by an increase in angular velocity such that the angular momentum is conserved.
Ex. A cockroach of mass 'm'is start moving, with velocity v on the circumference of a disc of mass' 'M" and radius'R'what will be angular velocity of disc.
Initially total angular momentum $=$ Final total angular momentum.
$$
0+0=m v R+\frac{m R^{2}}{2} \omega
$$
$\omega=(-) \frac{2 m v}{M R} \quad$ -ive angular velocity for opposite direction.\
(vi) The angular velocity of a planet around the Sun increases when it comes near the Sun. When a planet revolving around the Sun in an elliptical orbit comes near the Sun, the moment of inertia of the planet about the Sun decreases. In order to conserve angular momentum, the angular velocity shall increase. Similarly, when the planet is away from the Sun, there will be a decreases in the angular velocity.
(vii) The speed of the inner layers of the whirlwind in a tornado is alarmingly high, In a tornado, the moment of inertia of air will go on decreasing as the air moves the centre. This will be accompanied by an increase in angular velocity such that the angular momentum is conserved.
Ex. A cockroach of mass 'm'is start moving, with velocity v on the circumference of a disc of mass' 'M" and radius'R'what will be angular velocity of disc.
Initially total angular momentum $=$ Final total angular momentum.
$$
0+0=m v R+\frac{m R^{2}}{2} \omega
$$
$\omega=(-) \frac{2 m v}{M R} \quad$ -ive angular velocity for opposite direction.\
Ex. A rotating table has angular velocity '$\omega$' and moment of inertia I. Aperson of mass'm' stands of centre of rotating table. If the person moves rfrom the centre what will be angular velocity of rotating table. $\mathrm{I}_{1} \omega=\left(\mathrm{I}_{1}+\mathrm{mr}^{2}\right) \omega_{2} \quad$ or $\quad \omega_{2}=\frac{\mathrm{I}_{1} \omega}{\mathrm{I}_{1}+\mathrm{mr}^{2}}$
Ex. A horizontal disc is rotating about a vertical axis passing through its centre at the rate of 100 rev $\min .$ A blob of wax, of mass $20 \mathrm{gm},$ falls on the disc and sticks to it at a distance of $5 \mathrm{cm}$ from the axis. If the moment of inertia of the disc about the given axis is $2 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2},$ find the new frequency of rotation of the disc. $\begin{array}{ll}{\text { The M.I. of the disc, }} & {I_{1}=2 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}} \\ {\text { The M.I. of the blob of wax, }} & {\mathrm{I}_{2}=20 \times 10^{-3} \times(0.05)^{2}=0.5 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}}\end{array}$ Let the initial angular speed of the disc be $\omega=2 \pi n$ and let the final angular speed of the disc and blob of wax be $\omega^{\prime}=2 \pi n^{\prime}$ \text { Then, } \quad \mathrm{I}_{1} \omega=\left(\mathrm{I}_{1}+\mathrm{I}_{2}\right) \omega^{\prime} $\mathrm{I}_{1} \times 2 \pi \mathrm{n}=\left(\mathrm{I}_{1}+\mathrm{I}_{2}\right) 2 \pi \mathrm{n'}$ (The law of conservation of angular momentum) $\therefore 2 \times 10^{-4} \times 100=\left(2 \times 10^{-4}+0.5 \times 10^{-4}\right) \times n'$ so, $n^{\prime}=\frac{2}{2.5} \times 10^{2}=80 \mathrm{rev} / \mathrm{min}$
Ex. A solid cylinder of mass 'M'kg and radius 'R' is rotating along its axis with angular velocity $\omega$ without friction. A particle of mass' 'm'moving at v m/sec collide against the cylinder and sticks to it. Then calculate angular velocity and angular momentum of cylinder and initial and final kinetic energy of system? Intial momentum of cylinder $=\mathrm{I} \omega \quad$ Intial momentum of particle $=\mathrm{m} \mathrm{v} \mathrm{R}$ Before sticking total angular momentum $\mathrm{J}_{1}=\mathrm{I} \omega+\mathrm{mvR}$ After sticking total angular momentum $\quad \mathrm{J}_{2}=\left(\mathrm{I}+\mathrm{mR}^{2}\right) \omega^{\prime}$ if $\tau=0 \quad$ then $\quad J_{1}=J_{2}$ Angular velocity $\quad \omega^{\prime}=\frac{I \omega+m v R}{I+m R^{2}}$ Initial kinetic energy of system $=\frac{1}{2} \mathrm{I} \omega^{2}+\frac{1}{2} \mathrm{mv}^{2}$ Final kinetic energy of system $\quad=\frac{1}{2}\left(\mathrm{I}+\mathrm{mR}^{2}\right) \omega^{2}$
Ex. If the earth were suddenly to shrink to half its size (its mass remaining const) what would be the length of a day. Sol. $\quad \mathrm{I}_{1} \omega_{1}=\mathrm{I}_{2} \omega_{2} \quad$ so $\quad \frac{2}{5} \mathrm{MR}^{2} \times \frac{2 \pi}{\mathrm{T}_{1}}=\frac{2}{5} \mathrm{M}\left(\frac{\mathrm{R}}{2}\right)^{2} \frac{2 \pi}{\mathrm{T}_{2}}$ hence $\mathrm{T}_{1}=24 \mathrm{hr} \quad \mathrm{T}_{2}=6 \mathrm{hr}$
Ex. In which of the following cases, it is most difficult to rotate the rod? Sol. $\quad(\mathrm{c})$ as $\mathrm{I}$ is maximum.
Sol. $\quad(\mathrm{c})$ as $\mathrm{I}$ is maximum.
Ex. A thin meter scale is kept vertical by placing its one end on floor keeping the end in contact stationary it is allowed to fall. Find the velocity of its upper end when it hit the floor. Sol. $\quad \mathrm{mgh}=\frac{1}{2} \mathrm{I} \omega^{2} \quad$ where $\mathrm{h}=\frac{\ell}{2}, \mathrm{I}=\frac{\mathrm{m} \ell^{2}}{3}, \omega=\frac{\mathrm{v}}{\ell}$ [Loss is P.E. = Rotational K.E.] $\frac{\mathrm{mg} \ell}{2}=\frac{1}{2} \times \frac{\mathrm{m} \ell^{2}}{3} \times \frac{\mathrm{v}^{2}}{\ell^{2}} \quad \mathrm{v}=\sqrt{3 \mathrm{g} \ell}$
Ex. A particle is moving in $x-y$ plane and the components of its velocity along $x$ and $y$ axis are $v_{x}$ and $v_{y}$. Find the angular momentum about the origin. We know that angular momentum of a particle $\vec{J}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}=\overrightarrow{\mathrm{r}} \times \mathrm{m} \overrightarrow{\mathrm{v}}=\mathrm{m}(\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{v}})$ $=\mathrm{m}\left|\begin{array}{ccc}{\mathrm{i}} & {\mathrm{j}} & {\mathrm{k}} \\ {\mathrm{x}} & {\mathrm{y}} & {\mathrm{z}} \\ {\mathrm{V}_{\mathrm{x}}} & {\mathrm{V}_{\mathrm{y}}} & {\mathrm{V}_{\mathrm{z}}}\end{array}\right|=\mathrm{m}\left|\begin{array}{ccc}{\mathrm{i}} & {\mathrm{j}} & {\mathrm{k}} \\ {\mathrm{x}} & {\mathrm{y}} & {\mathrm{o}} \\ {\mathrm{V}_{\mathrm{x}}} & {\mathrm{V}_{\mathrm{y}}} & {\mathrm{o}}\end{array}\right|=\mathrm{m}\left(\mathrm{x} \vee_{\mathrm{y}}-\mathrm{y} \mathrm{v}_{\mathrm{x}}\right) \hat{\mathrm{k}}$
Ex. A ring of mass $10 \mathrm{kg}$ and diameter 0.4 $\mathrm{m}$ is rotating about its geometrical axis at 1200 rot./min. Find its moment of inertia and angular momentum. M.I. of a ring about its geometrical axis $=$ M.I. of ring an axis passing through its centre and $\quad$ perpendicular to its plane. $=M R^{2}=10(0.2)^{2}=10 \times 0.04=0.4 \mathrm{kg}-\mathrm{m}^{2}$ Now Angular momentum, $J=$ I. $\omega=I \frac{2 \pi n}{t}=0.4 \times \frac{2 \pi \times 1200}{60}=50.24 \mathrm{J-sec}$
Ex. A homogeneous rod $\mathrm{AB}$ of length $\mathrm{L}$ and mass $\mathrm{M}$ is pivoted at the centre 0 in such a way that it can rotate freely in a vertical plane. The rod $\mathrm{AB}$ is initially in horizontal position. An insect $\mathrm{S}$ of same mass falls vertically with a speed $\mathrm{V}$ at the point c, midway between points 0 and $\mathrm{B}$. Immediately after the insect falls, the angular velocity of the system is Sol. By Law of conservation of angular momentum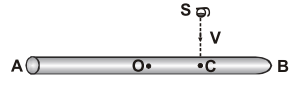 $\left(\sum \mathrm{mvr}\right)_{\mathrm{about} 0}=\left(\begin{array}{c}{\mathrm{I}_{\mathrm{system}}} \\ {\mathrm{about} 0}\end{array}\right) \omega$
$\Rightarrow M V \frac{L}{4}=\left[\frac{M L^{2}}{12}+M\left(\frac{L}{4}\right)^{2}\right] \omega \Rightarrow \quad M V \frac{L}{4}=M L^{2}\left(\frac{1}{12}+\frac{1}{16}\right) \omega$
$\Rightarrow \mathrm{MV} \frac{\mathrm{L}}{4}=\mathrm{ML}^{2}\left(\frac{4+3}{48}\right) \omega \quad \Rightarrow \quad \omega=\frac{12}{7} \frac{\mathrm{V}}{\mathrm{L}}$
$\left(\sum \mathrm{mvr}\right)_{\mathrm{about} 0}=\left(\begin{array}{c}{\mathrm{I}_{\mathrm{system}}} \\ {\mathrm{about} 0}\end{array}\right) \omega$
$\Rightarrow M V \frac{L}{4}=\left[\frac{M L^{2}}{12}+M\left(\frac{L}{4}\right)^{2}\right] \omega \Rightarrow \quad M V \frac{L}{4}=M L^{2}\left(\frac{1}{12}+\frac{1}{16}\right) \omega$
$\Rightarrow \mathrm{MV} \frac{\mathrm{L}}{4}=\mathrm{ML}^{2}\left(\frac{4+3}{48}\right) \omega \quad \Rightarrow \quad \omega=\frac{12}{7} \frac{\mathrm{V}}{\mathrm{L}}$
Introduction to Rotational Dynamics Moment of Inertia Moment of Inertia: Perpendicular and Parallel axis theorem Radius of Gyration Law of Conservation of Angular Momentum Conservation of Angular Momentum Examples Kinetic Energy of a Rotating Body Work done in rotatory Motion Rotational Power Combine Translational and Rotational Motion Rolling without slipping Rolling on a plane surface Rolling on a Inclined Plane For Latest updates, Subscribe our Youtube Channel
 (i) A point mass is tied to one end of a cord whose other end passes through a vertical hollow tube, caught in one hand. The point mass is being rotated in a horizontal circle. The cord is then pulled down so that the radius of the circle reduces.
Here the force on the point mass due to cord is radial and hence the torque about the center of rotation is zero therefore, the angular momentum must remain constant as the cord shortend.
As cord is pulled down, the point mass rotates faster than before. The reason is that by shortening the radius of the circle, the moment of inertia of point mass about axis of rotation decreases
$\mathrm{I}_{\mathrm{i}} \omega_{\mathrm{i}}=\mathrm{I}_{\mathrm{f}} \omega_{\mathrm{f}} \quad \mathrm{I}_{\mathrm{i}}>\mathrm{I}_{\mathrm{f}} \quad$ so $\omega_{\mathrm{i}}<\omega_{\mathrm{f}}$
(ii) A man with his arms outstretched and holding heavy bells in each
hand, is standing at the centre of a rotating table. When the man pulls his arms,
the speed of rotation of the table increases. The reason is that on pulling the
(i) A point mass is tied to one end of a cord whose other end passes through a vertical hollow tube, caught in one hand. The point mass is being rotated in a horizontal circle. The cord is then pulled down so that the radius of the circle reduces.
Here the force on the point mass due to cord is radial and hence the torque about the center of rotation is zero therefore, the angular momentum must remain constant as the cord shortend.
As cord is pulled down, the point mass rotates faster than before. The reason is that by shortening the radius of the circle, the moment of inertia of point mass about axis of rotation decreases
$\mathrm{I}_{\mathrm{i}} \omega_{\mathrm{i}}=\mathrm{I}_{\mathrm{f}} \omega_{\mathrm{f}} \quad \mathrm{I}_{\mathrm{i}}>\mathrm{I}_{\mathrm{f}} \quad$ so $\omega_{\mathrm{i}}<\omega_{\mathrm{f}}$
(ii) A man with his arms outstretched and holding heavy bells in each
hand, is standing at the centre of a rotating table. When the man pulls his arms,
the speed of rotation of the table increases. The reason is that on pulling the arms, the distance R of the dumbells from the axis of rotation decreases and so the moment of inertia decreases. Therefore, by conservation of angular momentum, the angular velocity increases.
arms, the distance R of the dumbells from the axis of rotation decreases and so the moment of inertia decreases. Therefore, by conservation of angular momentum, the angular velocity increases.
 (iii) When a diver jumps into water from a height, he does not keep his body straight but pulls in his arms and legs towards the centre of his body. On doing so, the moment of inertia I of his body decreases. But since the angular momentum I $\omega$ remains constant, his angular velocity $\omega$ correspondingly increases.
Hence during jumping he can rotate his body in the air.
(iv) In the same way, the ice skater and the ballet dancer increase or decrease the angular velocity of spin about a vertical axis by pulling or
extending out their limbs.
(iii) When a diver jumps into water from a height, he does not keep his body straight but pulls in his arms and legs towards the centre of his body. On doing so, the moment of inertia I of his body decreases. But since the angular momentum I $\omega$ remains constant, his angular velocity $\omega$ correspondingly increases.
Hence during jumping he can rotate his body in the air.
(iv) In the same way, the ice skater and the ballet dancer increase or decrease the angular velocity of spin about a vertical axis by pulling or
extending out their limbs.
 (v) A: axis is horizontal; angular momentum about vertical axis $=0$. B: axis is vertical; angular momentum about vertical axis is still zero; man and chair spin in direction opposite to spin of the wheel.
(v) A: axis is horizontal; angular momentum about vertical axis $=0$. B: axis is vertical; angular momentum about vertical axis is still zero; man and chair spin in direction opposite to spin of the wheel.
 (vi) The angular velocity of a planet around the Sun increases when it comes near the Sun. When a planet revolving around the Sun in an elliptical orbit comes near the Sun, the moment of inertia of the planet about the Sun decreases. In order to conserve angular momentum, the angular velocity shall increase. Similarly, when the planet is away from the Sun, there will be a decreases in the angular velocity.
(vii) The speed of the inner layers of the whirlwind in a tornado is alarmingly high, In a tornado, the moment of inertia of air will go on decreasing as the air moves the centre. This will be accompanied by an increase in angular velocity such that the angular momentum is conserved.
Ex. A cockroach of mass 'm'is start moving, with velocity v on the circumference of a disc of mass' 'M" and radius'R'what will be angular velocity of disc.
Initially total angular momentum $=$ Final total angular momentum.
$$
0+0=m v R+\frac{m R^{2}}{2} \omega
$$
$\omega=(-) \frac{2 m v}{M R} \quad$ -ive angular velocity for opposite direction.\
(vi) The angular velocity of a planet around the Sun increases when it comes near the Sun. When a planet revolving around the Sun in an elliptical orbit comes near the Sun, the moment of inertia of the planet about the Sun decreases. In order to conserve angular momentum, the angular velocity shall increase. Similarly, when the planet is away from the Sun, there will be a decreases in the angular velocity.
(vii) The speed of the inner layers of the whirlwind in a tornado is alarmingly high, In a tornado, the moment of inertia of air will go on decreasing as the air moves the centre. This will be accompanied by an increase in angular velocity such that the angular momentum is conserved.
Ex. A cockroach of mass 'm'is start moving, with velocity v on the circumference of a disc of mass' 'M" and radius'R'what will be angular velocity of disc.
Initially total angular momentum $=$ Final total angular momentum.
$$
0+0=m v R+\frac{m R^{2}}{2} \omega
$$
$\omega=(-) \frac{2 m v}{M R} \quad$ -ive angular velocity for opposite direction.\
Ex. A rotating table has angular velocity '$\omega$' and moment of inertia I. Aperson of mass'm' stands of centre of rotating table. If the person moves rfrom the centre what will be angular velocity of rotating table. $\mathrm{I}_{1} \omega=\left(\mathrm{I}_{1}+\mathrm{mr}^{2}\right) \omega_{2} \quad$ or $\quad \omega_{2}=\frac{\mathrm{I}_{1} \omega}{\mathrm{I}_{1}+\mathrm{mr}^{2}}$
Ex. A horizontal disc is rotating about a vertical axis passing through its centre at the rate of 100 rev $\min .$ A blob of wax, of mass $20 \mathrm{gm},$ falls on the disc and sticks to it at a distance of $5 \mathrm{cm}$ from the axis. If the moment of inertia of the disc about the given axis is $2 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2},$ find the new frequency of rotation of the disc. $\begin{array}{ll}{\text { The M.I. of the disc, }} & {I_{1}=2 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}} \\ {\text { The M.I. of the blob of wax, }} & {\mathrm{I}_{2}=20 \times 10^{-3} \times(0.05)^{2}=0.5 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}}\end{array}$ Let the initial angular speed of the disc be $\omega=2 \pi n$ and let the final angular speed of the disc and blob of wax be $\omega^{\prime}=2 \pi n^{\prime}$ \text { Then, } \quad \mathrm{I}_{1} \omega=\left(\mathrm{I}_{1}+\mathrm{I}_{2}\right) \omega^{\prime} $\mathrm{I}_{1} \times 2 \pi \mathrm{n}=\left(\mathrm{I}_{1}+\mathrm{I}_{2}\right) 2 \pi \mathrm{n'}$ (The law of conservation of angular momentum) $\therefore 2 \times 10^{-4} \times 100=\left(2 \times 10^{-4}+0.5 \times 10^{-4}\right) \times n'$ so, $n^{\prime}=\frac{2}{2.5} \times 10^{2}=80 \mathrm{rev} / \mathrm{min}$
Ex. A solid cylinder of mass 'M'kg and radius 'R' is rotating along its axis with angular velocity $\omega$ without friction. A particle of mass' 'm'moving at v m/sec collide against the cylinder and sticks to it. Then calculate angular velocity and angular momentum of cylinder and initial and final kinetic energy of system? Intial momentum of cylinder $=\mathrm{I} \omega \quad$ Intial momentum of particle $=\mathrm{m} \mathrm{v} \mathrm{R}$ Before sticking total angular momentum $\mathrm{J}_{1}=\mathrm{I} \omega+\mathrm{mvR}$ After sticking total angular momentum $\quad \mathrm{J}_{2}=\left(\mathrm{I}+\mathrm{mR}^{2}\right) \omega^{\prime}$ if $\tau=0 \quad$ then $\quad J_{1}=J_{2}$ Angular velocity $\quad \omega^{\prime}=\frac{I \omega+m v R}{I+m R^{2}}$ Initial kinetic energy of system $=\frac{1}{2} \mathrm{I} \omega^{2}+\frac{1}{2} \mathrm{mv}^{2}$ Final kinetic energy of system $\quad=\frac{1}{2}\left(\mathrm{I}+\mathrm{mR}^{2}\right) \omega^{2}$
Ex. If the earth were suddenly to shrink to half its size (its mass remaining const) what would be the length of a day. Sol. $\quad \mathrm{I}_{1} \omega_{1}=\mathrm{I}_{2} \omega_{2} \quad$ so $\quad \frac{2}{5} \mathrm{MR}^{2} \times \frac{2 \pi}{\mathrm{T}_{1}}=\frac{2}{5} \mathrm{M}\left(\frac{\mathrm{R}}{2}\right)^{2} \frac{2 \pi}{\mathrm{T}_{2}}$ hence $\mathrm{T}_{1}=24 \mathrm{hr} \quad \mathrm{T}_{2}=6 \mathrm{hr}$
Ex. In which of the following cases, it is most difficult to rotate the rod?
 Sol. $\quad(\mathrm{c})$ as $\mathrm{I}$ is maximum.
Sol. $\quad(\mathrm{c})$ as $\mathrm{I}$ is maximum.
Ex. A thin meter scale is kept vertical by placing its one end on floor keeping the end in contact stationary it is allowed to fall. Find the velocity of its upper end when it hit the floor. Sol. $\quad \mathrm{mgh}=\frac{1}{2} \mathrm{I} \omega^{2} \quad$ where $\mathrm{h}=\frac{\ell}{2}, \mathrm{I}=\frac{\mathrm{m} \ell^{2}}{3}, \omega=\frac{\mathrm{v}}{\ell}$ [Loss is P.E. = Rotational K.E.] $\frac{\mathrm{mg} \ell}{2}=\frac{1}{2} \times \frac{\mathrm{m} \ell^{2}}{3} \times \frac{\mathrm{v}^{2}}{\ell^{2}} \quad \mathrm{v}=\sqrt{3 \mathrm{g} \ell}$
Ex. A particle is moving in $x-y$ plane and the components of its velocity along $x$ and $y$ axis are $v_{x}$ and $v_{y}$. Find the angular momentum about the origin. We know that angular momentum of a particle $\vec{J}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}=\overrightarrow{\mathrm{r}} \times \mathrm{m} \overrightarrow{\mathrm{v}}=\mathrm{m}(\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{v}})$ $=\mathrm{m}\left|\begin{array}{ccc}{\mathrm{i}} & {\mathrm{j}} & {\mathrm{k}} \\ {\mathrm{x}} & {\mathrm{y}} & {\mathrm{z}} \\ {\mathrm{V}_{\mathrm{x}}} & {\mathrm{V}_{\mathrm{y}}} & {\mathrm{V}_{\mathrm{z}}}\end{array}\right|=\mathrm{m}\left|\begin{array}{ccc}{\mathrm{i}} & {\mathrm{j}} & {\mathrm{k}} \\ {\mathrm{x}} & {\mathrm{y}} & {\mathrm{o}} \\ {\mathrm{V}_{\mathrm{x}}} & {\mathrm{V}_{\mathrm{y}}} & {\mathrm{o}}\end{array}\right|=\mathrm{m}\left(\mathrm{x} \vee_{\mathrm{y}}-\mathrm{y} \mathrm{v}_{\mathrm{x}}\right) \hat{\mathrm{k}}$
Ex. A ring of mass $10 \mathrm{kg}$ and diameter 0.4 $\mathrm{m}$ is rotating about its geometrical axis at 1200 rot./min. Find its moment of inertia and angular momentum. M.I. of a ring about its geometrical axis $=$ M.I. of ring an axis passing through its centre and $\quad$ perpendicular to its plane. $=M R^{2}=10(0.2)^{2}=10 \times 0.04=0.4 \mathrm{kg}-\mathrm{m}^{2}$ Now Angular momentum, $J=$ I. $\omega=I \frac{2 \pi n}{t}=0.4 \times \frac{2 \pi \times 1200}{60}=50.24 \mathrm{J-sec}$
Ex. A homogeneous rod $\mathrm{AB}$ of length $\mathrm{L}$ and mass $\mathrm{M}$ is pivoted at the centre 0 in such a way that it can rotate freely in a vertical plane. The rod $\mathrm{AB}$ is initially in horizontal position. An insect $\mathrm{S}$ of same mass falls vertically with a speed $\mathrm{V}$ at the point c, midway between points 0 and $\mathrm{B}$. Immediately after the insect falls, the angular velocity of the system is Sol. By Law of conservation of angular momentum
 $\left(\sum \mathrm{mvr}\right)_{\mathrm{about} 0}=\left(\begin{array}{c}{\mathrm{I}_{\mathrm{system}}} \\ {\mathrm{about} 0}\end{array}\right) \omega$
$\Rightarrow M V \frac{L}{4}=\left[\frac{M L^{2}}{12}+M\left(\frac{L}{4}\right)^{2}\right] \omega \Rightarrow \quad M V \frac{L}{4}=M L^{2}\left(\frac{1}{12}+\frac{1}{16}\right) \omega$
$\Rightarrow \mathrm{MV} \frac{\mathrm{L}}{4}=\mathrm{ML}^{2}\left(\frac{4+3}{48}\right) \omega \quad \Rightarrow \quad \omega=\frac{12}{7} \frac{\mathrm{V}}{\mathrm{L}}$
$\left(\sum \mathrm{mvr}\right)_{\mathrm{about} 0}=\left(\begin{array}{c}{\mathrm{I}_{\mathrm{system}}} \\ {\mathrm{about} 0}\end{array}\right) \omega$
$\Rightarrow M V \frac{L}{4}=\left[\frac{M L^{2}}{12}+M\left(\frac{L}{4}\right)^{2}\right] \omega \Rightarrow \quad M V \frac{L}{4}=M L^{2}\left(\frac{1}{12}+\frac{1}{16}\right) \omega$
$\Rightarrow \mathrm{MV} \frac{\mathrm{L}}{4}=\mathrm{ML}^{2}\left(\frac{4+3}{48}\right) \omega \quad \Rightarrow \quad \omega=\frac{12}{7} \frac{\mathrm{V}}{\mathrm{L}}$
Introduction to Rotational Dynamics Moment of Inertia Moment of Inertia: Perpendicular and Parallel axis theorem Radius of Gyration Law of Conservation of Angular Momentum Conservation of Angular Momentum Examples Kinetic Energy of a Rotating Body Work done in rotatory Motion Rotational Power Combine Translational and Rotational Motion Rolling without slipping Rolling on a plane surface Rolling on a Inclined Plane For Latest updates, Subscribe our Youtube Channel
Comments
Michael Paul [email protected]
June 14, 2020, 9:29 p.m.
A puzzle, concerning the conservation of angular momentum. A mass 'm' is rotating horizontally at a given velocity 'v' at a given radius 'r'. The mass has energy of J = 1/2*m*v^2 Now let the radius gradually reduce by one half. At the new radius the velocity is a factor of two faster. This gives the mass a larger energy by a factor of four. Where did the mass get the additional energy from?
