Here, you will learn in detail about Rotational Dynamics and Moment of Inertia. Study about rigid bodies and system of particles in this chapter
Rotatory Motion
Moment of Force or torque
Rotational Equilibrium
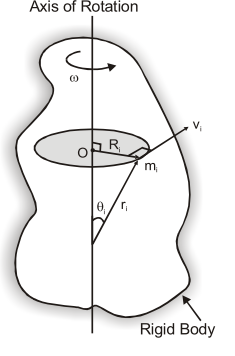
RIGID BODY
System of particle which does not change its shape under the influence of ordinary external force and distance between the particle does not change with respect to time.
(i) No body in universe is perfectly rigid. However the bodies in which strain effect is quite
negigible under the influence of external force may be said to be rigid bodies e.g. earth, billiard ball etc.
(ii) The internal structure of a rigid body and its shape and size do not change in state of motion.
Rotatory Motion
A body rotating about a fixed axis then every particle of the body moves in a circle and the centres of all these circles lie at axis of rotation.
$\overrightarrow{\mathrm{v}}_{\mathrm{i}}=\mathrm{v}$ elocity of $\mathrm{i}^{\text {th }}$ particle of mass $\mathrm{m}_{\mathrm{i}}$
$\overrightarrow{\mathrm{r}_{\mathrm{i}}}=$ position vector of $\mathrm{i}^{\mathrm{th}}$particle
$\mathrm{R}_{\mathrm{i}}=$ perpendicular distance of $\mathrm{i}^{\mathrm{ith}}$ particle from axis of rotation.
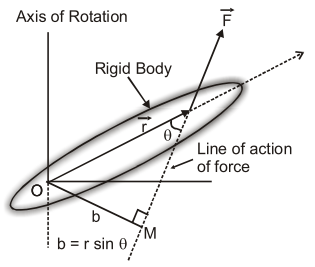
MOMENT OF FORCE OR TORQUE
If a hinged or suspended or pivoted body tends to rotate under the action of force, it said to be acted on by a torque:
The moment of a force or the torque, about an axis of rotation is equal to the product of the force and perpendicular distance of the line of the action of the force from axis of rotation.
The magnitude of torque will be
$$
\tau=F . b \quad=F r \sin \theta
$$
$b=r \sin \theta$ is known as lever arm or moment arm
Unit: $\quad$ M.K.S. : $N-m$
C. G.S. : dyne-cm
Dimension: $M L^{2} T^{-2}$
vector form $\vec{\tau}=\vec{r} \times \vec{F}=r F \sin \theta \hat{n},$ where $\theta$ is angle between $\vec{r}$ and
$\vec{F}$ and $\hat{n}$ is unit vector perpendicular to the plane of $\vec{r}$ and $\vec{F}$.
Torque is an axial vector i.e. its direction is always perpendicular the plane containing vector $\overrightarrow{\mathrm{r}}$ and $\overrightarrow{\mathrm{F}}$ in accordance with right hand rule.
If the torque rotates the body in anticlock wise direction, the torque is positive and if the torque rotates the body in clock-wise direction, the torque will be negative.
Torque is Minimum
When $|\sin \theta|=\min =0$
i.e., $\theta=0^{\circ}$ or $180^{\circ}$
i.e., $\overrightarrow{\mathrm{F}}$ is collinear with $\overrightarrow{\mathrm{r}}$
And $\tau_{\min }=0$
Torque is Maximum
When $|\sin \theta|=\max =1$
i.e., $\theta=90^{\circ}$
i.e., $\overrightarrow{\mathrm{F}}$ is orthogonal to $\overrightarrow{\mathrm{r}}$
And $\tau_{\max }=\mathrm{Fr}$
If a body is acted upon by more than one torque, the total torque is the vector sum of each torque.
$$
\vec{\tau}=\vec{\tau}_{1}+\vec{\tau}_{2}+\vec{\tau}_{2}+\ldots \ldots \ldots+\vec{\tau}_{n}+\vec{\tau}_{n} \vec{\tau}=\sum_{i=1}^{n} \vec{\tau}_{i}
$$
Rotational equilibrium $\sum_{i=1}^{n} \vec{\tau}_{i}=0$
$$
\quad \quad \tau=\mathrm{I} \alpha
$$
I- Moment of inertia with respect to axis of rotation.
$\alpha$ - Angular acceleration with respect to axis of rotation.
$\vec{\tau}=\frac{d \vec{J}}{d t},$ where $\vec{J}$ is angular momentum.
The more is the value of b, the more will be torque and easier to rotate the body.
(i) The handle of screw driver is taken thick.
(ii) In villages the handle of flour-mill is placed near the circumference.
(iii) The handle of handpump is kept-long.
(iv) The rinch used for opening the tap, is kept-tong.
$$
\begin{aligned} \tau=\text { const. } & \text { i.e. } \quad F r \sin \theta=\text { const. } \\ & F=\frac{\text { Const. }}{r \sin \theta} \end{aligned}
$$
i.e. longer the arm and greater sin $\theta$, lesser will be the force required for producing desired rotational effect.
COUPLE OF FORCES
When two forces equal in magnitude but opposite in direction acting at two different points of a body they
form couple. This couple tries to rotate body.
$$
\begin{array}{l}{\tau=F \cdot b} \\ {b=d \sin \theta}\end{array}
$$
Introduction to Rotational Dynamics
Moment of Inertia
Moment of Inertia: Perpendicular and Parallel axis theorem
Radius of Gyration
Law of Conservation of Angular Momentum
Conservation of Angular Momentum Examples
Kinetic Energy of a Rotating Body
Work done in rotatory Motion
Rotational Power
Combine Translational and Rotational Motion
Rolling without slipping
Rolling on a plane surface
Rolling on a Inclined Plane
MOMENT OF FORCE OR TORQUE
If a hinged or suspended or pivoted body tends to rotate under the action of force, it said to be acted on by a torque:
The moment of a force or the torque, about an axis of rotation is equal to the product of the force and perpendicular distance of the line of the action of the force from axis of rotation.
The magnitude of torque will be
$$
\tau=F . b \quad=F r \sin \theta
$$
$b=r \sin \theta$ is known as lever arm or moment arm
Unit: $\quad$ M.K.S. : $N-m$
C. G.S. : dyne-cm
Dimension: $M L^{2} T^{-2}$
vector form $\vec{\tau}=\vec{r} \times \vec{F}=r F \sin \theta \hat{n},$ where $\theta$ is angle between $\vec{r}$ and
$\vec{F}$ and $\hat{n}$ is unit vector perpendicular to the plane of $\vec{r}$ and $\vec{F}$.
Torque is an axial vector i.e. its direction is always perpendicular the plane containing vector $\overrightarrow{\mathrm{r}}$ and $\overrightarrow{\mathrm{F}}$ in accordance with right hand rule.
If the torque rotates the body in anticlock wise direction, the torque is positive and if the torque rotates the body in clock-wise direction, the torque will be negative.
Torque is Minimum
When $|\sin \theta|=\min =0$
i.e., $\theta=0^{\circ}$ or $180^{\circ}$
i.e., $\overrightarrow{\mathrm{F}}$ is collinear with $\overrightarrow{\mathrm{r}}$
And $\tau_{\min }=0$
Torque is Maximum
When $|\sin \theta|=\max =1$
i.e., $\theta=90^{\circ}$
i.e., $\overrightarrow{\mathrm{F}}$ is orthogonal to $\overrightarrow{\mathrm{r}}$
And $\tau_{\max }=\mathrm{Fr}$
If a body is acted upon by more than one torque, the total torque is the vector sum of each torque.
$$
\vec{\tau}=\vec{\tau}_{1}+\vec{\tau}_{2}+\vec{\tau}_{2}+\ldots \ldots \ldots+\vec{\tau}_{n}+\vec{\tau}_{n} \vec{\tau}=\sum_{i=1}^{n} \vec{\tau}_{i}
$$
Rotational equilibrium $\sum_{i=1}^{n} \vec{\tau}_{i}=0$
$$
\quad \quad \tau=\mathrm{I} \alpha
$$
I- Moment of inertia with respect to axis of rotation.
$\alpha$ - Angular acceleration with respect to axis of rotation.
$\vec{\tau}=\frac{d \vec{J}}{d t},$ where $\vec{J}$ is angular momentum.
The more is the value of b, the more will be torque and easier to rotate the body.
(i) The handle of screw driver is taken thick.
(ii) In villages the handle of flour-mill is placed near the circumference.
(iii) The handle of handpump is kept-long.
(iv) The rinch used for opening the tap, is kept-tong.
$$
\begin{aligned} \tau=\text { const. } & \text { i.e. } \quad F r \sin \theta=\text { const. } \\ & F=\frac{\text { Const. }}{r \sin \theta} \end{aligned}
$$
i.e. longer the arm and greater sin $\theta$, lesser will be the force required for producing desired rotational effect.
COUPLE OF FORCES
When two forces equal in magnitude but opposite in direction acting at two different points of a body they
form couple. This couple tries to rotate body.
$$
\begin{array}{l}{\tau=F \cdot b} \\ {b=d \sin \theta}\end{array}
$$
Introduction to Rotational Dynamics
Moment of Inertia
Moment of Inertia: Perpendicular and Parallel axis theorem
Radius of Gyration
Law of Conservation of Angular Momentum
Conservation of Angular Momentum Examples
Kinetic Energy of a Rotating Body
Work done in rotatory Motion
Rotational Power
Combine Translational and Rotational Motion
Rolling without slipping
Rolling on a plane surface
Rolling on a Inclined Plane