Theorems of Moment of Inertia: Parallel and Perpendicular Axis Theorem
 2. Parallel axes theorem : [For all types of bodies]
According to this principle, the moment of inertia of a rigid body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of mass and the product of the mass of the body and the square of
the distance between the two axis.
2. Parallel axes theorem : [For all types of bodies]
According to this principle, the moment of inertia of a rigid body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of mass and the product of the mass of the body and the square of
the distance between the two axis.
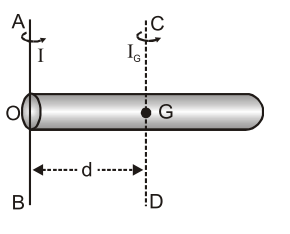 $\mathrm{I}=\mathrm{I}_{\mathrm{g}}+\mathrm{Md}^{2}$
Ex. The diameter of flywheel increases by $1 \%$. Find the percentage increase in moment of inertia about axis of symmetry.
Sol. The moment of inertia of flywheel is given by, $\quad \mathrm{I}=\mathrm{MR}^{2}$
Taking log, $\quad \log \mathrm{I}=\log \mathrm{M}+2 \log \mathrm{R}$
Differentiating, $\quad \frac{\mathrm{d} \mathrm{I}}{\mathrm{I}}=0+2 \frac{\mathrm{d} \mathrm{R}}{\mathrm{R}}$
$\therefore \quad \%$ change in moment of inertia $=\frac{d I}{I} \times 100=2 \times 1 \%=2 \%$
Ex. The moment of inertia of sphere is $20 \mathrm{kg}-\mathrm{m}^{2}$ about the diameter. Find the moment of inertia about any tangent.\
Sol. According to the theorem of parallel axes, we have
$$
\begin{aligned} \mathrm{I}=\mathrm{I}_{6}+\mathrm{Ma}^{2}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{MR}^{2} &(\because \mathrm{d}=\mathrm{R}) \\=&\left.\frac{7}{5} \mathrm{MR}^{2}=\frac{7}{2} \times \frac{2}{5} \mathrm{MR}^{2}=\frac{7}{2} \times 20=70 \mathrm{kg}-\mathrm{m}^{2} \quad \text { (Given } \frac{2}{5} \mathrm{MR}^{2}=20\right) \end{aligned}
$$
Ex. If the moment of inertia of a disc about an axis tangentially and parallel to its surface be I, what will be the moment of inertia about the axis tangential but perpendicular to the surface.
Sol. According to the theorem of parallel axes, the moment of inertia of the disc about an axis tangentially
and parallel to the surface is given by-
$$
\mathrm{I}=\mathrm{I}_{\|}=\frac{\mathrm{MR}^{2}}{4}+\mathrm{MR}^{2}=\frac{5}{4} \mathrm{MR}^{2}
$$
The moment of inertia of the disc about an axis tangential but perpendicular to the surface is given by
$$
\mathrm{I}^{\prime}=\frac{\mathrm{MR}^{2}}{2}+\mathrm{MR}^{2}=\frac{3}{2} \mathrm{MR}^{2}=\frac{6}{5}\left[\frac{5}{4} \mathrm{MR}^{2}\right]=\frac{6}{5} \mathrm{I}
$$
Ex. Find the moment of inertia of a uniform semicircular wire of mass $M$ and radius $r$ about a line perpendicular to the plane of the wire through the center.
$\mathrm{I}=\mathrm{I}_{\mathrm{g}}+\mathrm{Md}^{2}$
Ex. The diameter of flywheel increases by $1 \%$. Find the percentage increase in moment of inertia about axis of symmetry.
Sol. The moment of inertia of flywheel is given by, $\quad \mathrm{I}=\mathrm{MR}^{2}$
Taking log, $\quad \log \mathrm{I}=\log \mathrm{M}+2 \log \mathrm{R}$
Differentiating, $\quad \frac{\mathrm{d} \mathrm{I}}{\mathrm{I}}=0+2 \frac{\mathrm{d} \mathrm{R}}{\mathrm{R}}$
$\therefore \quad \%$ change in moment of inertia $=\frac{d I}{I} \times 100=2 \times 1 \%=2 \%$
Ex. The moment of inertia of sphere is $20 \mathrm{kg}-\mathrm{m}^{2}$ about the diameter. Find the moment of inertia about any tangent.\
Sol. According to the theorem of parallel axes, we have
$$
\begin{aligned} \mathrm{I}=\mathrm{I}_{6}+\mathrm{Ma}^{2}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{MR}^{2} &(\because \mathrm{d}=\mathrm{R}) \\=&\left.\frac{7}{5} \mathrm{MR}^{2}=\frac{7}{2} \times \frac{2}{5} \mathrm{MR}^{2}=\frac{7}{2} \times 20=70 \mathrm{kg}-\mathrm{m}^{2} \quad \text { (Given } \frac{2}{5} \mathrm{MR}^{2}=20\right) \end{aligned}
$$
Ex. If the moment of inertia of a disc about an axis tangentially and parallel to its surface be I, what will be the moment of inertia about the axis tangential but perpendicular to the surface.
Sol. According to the theorem of parallel axes, the moment of inertia of the disc about an axis tangentially
and parallel to the surface is given by-
$$
\mathrm{I}=\mathrm{I}_{\|}=\frac{\mathrm{MR}^{2}}{4}+\mathrm{MR}^{2}=\frac{5}{4} \mathrm{MR}^{2}
$$
The moment of inertia of the disc about an axis tangential but perpendicular to the surface is given by
$$
\mathrm{I}^{\prime}=\frac{\mathrm{MR}^{2}}{2}+\mathrm{MR}^{2}=\frac{3}{2} \mathrm{MR}^{2}=\frac{6}{5}\left[\frac{5}{4} \mathrm{MR}^{2}\right]=\frac{6}{5} \mathrm{I}
$$
Ex. Find the moment of inertia of a uniform semicircular wire of mass $M$ and radius $r$ about a line perpendicular to the plane of the wire through the center.
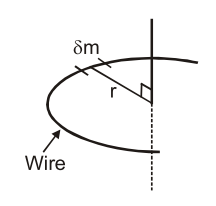 $\begin{array}{ll}{\text { Sol. }} & {\delta \mathrm{I}=\delta \mathrm{m} . \mathrm{r}^{2}} \\ {\qquad \begin{aligned} \mathrm{I} &=r^{2} \Sigma \delta \mathrm{m} \\ &=\mathrm{Mr}^{2} \end{aligned}}\end{array}$
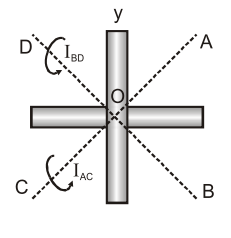
Ex. Two uniform, thin identical rods each of mass $M$ and length L are joined so as to form a cross as shown in fig. Find the moment of inertia of the cross about a bisector line AC.
Sol. Moment of inertia of cross about axis passing through $\mathrm{O}$ and perpendicualr to the plane of rods.
$\mathrm{I}_{0}=\frac{\mathrm{ML}^{2}}{12}+\frac{\mathrm{ML}^{2}}{12}$
With the help of theorem of perpendicular axes
$$
\begin{aligned} 2 \mathrm{I}_{\mathrm{AC}}+\mathrm{I}_{\mathrm{BD}}=\mathrm{I}_{0} & \text { c. } \\ \text { or } & \mathrm{I}_{\mathrm{AC}}=\frac{\mathrm{I}_{0}}{2}=\frac{\mathrm{ML}^{2}}{24} &\left(\mathrm{I}_{\mathrm{AC}}=\mathrm{I}_{\mathrm{BD}}\right) \end{aligned}
$$
$\begin{array}{ll}{\text { Sol. }} & {\delta \mathrm{I}=\delta \mathrm{m} . \mathrm{r}^{2}} \\ {\qquad \begin{aligned} \mathrm{I} &=r^{2} \Sigma \delta \mathrm{m} \\ &=\mathrm{Mr}^{2} \end{aligned}}\end{array}$
Ex. Two uniform, thin identical rods each of mass $M$ and length L are joined so as to form a cross as shown in fig. Find the moment of inertia of the cross about a bisector line AC.
Sol. Moment of inertia of cross about axis passing through $\mathrm{O}$ and perpendicualr to the plane of rods.
$\mathrm{I}_{0}=\frac{\mathrm{ML}^{2}}{12}+\frac{\mathrm{ML}^{2}}{12}$
With the help of theorem of perpendicular axes
$$
\begin{aligned} 2 \mathrm{I}_{\mathrm{AC}}+\mathrm{I}_{\mathrm{BD}}=\mathrm{I}_{0} & \text { c. } \\ \text { or } & \mathrm{I}_{\mathrm{AC}}=\frac{\mathrm{I}_{0}}{2}=\frac{\mathrm{ML}^{2}}{24} &\left(\mathrm{I}_{\mathrm{AC}}=\mathrm{I}_{\mathrm{BD}}\right) \end{aligned}
$$
 Introduction to Rotational Dynamics
Moment of Inertia
Moment of Inertia: Perpendicular and Parallel axis theorem
Radius of Gyration
Law of Conservation of Angular Momentum
Conservation of Angular Momentum Examples
Kinetic Energy of a Rotating Body
Work done in rotatory Motion
Rotational Power
Combine Translational and Rotational Motion
Rolling without slipping
Rolling on a plane surface
Rolling on a Inclined Plane
For Latest updates, Subscribe our Youtube Channel
Introduction to Rotational Dynamics
Moment of Inertia
Moment of Inertia: Perpendicular and Parallel axis theorem
Radius of Gyration
Law of Conservation of Angular Momentum
Conservation of Angular Momentum Examples
Kinetic Energy of a Rotating Body
Work done in rotatory Motion
Rotational Power
Combine Translational and Rotational Motion
Rolling without slipping
Rolling on a plane surface
Rolling on a Inclined Plane
For Latest updates, Subscribe our Youtube Channel
- Perpendicular axis theorem: [Only for laminar bodies] The sum of moments of inertia of a laminar body about any two mutually perpendicular axis in its plane is equal to its moment of inertia about an axis perpendicular to its plane and passing through the point intersection of the first two axis.
 2. Parallel axes theorem : [For all types of bodies]
According to this principle, the moment of inertia of a rigid body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of mass and the product of the mass of the body and the square of
the distance between the two axis.
2. Parallel axes theorem : [For all types of bodies]
According to this principle, the moment of inertia of a rigid body about any axis is equal to the sum of its moment of inertia about a parallel axis through its center of mass and the product of the mass of the body and the square of
the distance between the two axis.
 $\mathrm{I}=\mathrm{I}_{\mathrm{g}}+\mathrm{Md}^{2}$
Ex. The diameter of flywheel increases by $1 \%$. Find the percentage increase in moment of inertia about axis of symmetry.
Sol. The moment of inertia of flywheel is given by, $\quad \mathrm{I}=\mathrm{MR}^{2}$
Taking log, $\quad \log \mathrm{I}=\log \mathrm{M}+2 \log \mathrm{R}$
Differentiating, $\quad \frac{\mathrm{d} \mathrm{I}}{\mathrm{I}}=0+2 \frac{\mathrm{d} \mathrm{R}}{\mathrm{R}}$
$\therefore \quad \%$ change in moment of inertia $=\frac{d I}{I} \times 100=2 \times 1 \%=2 \%$
Ex. The moment of inertia of sphere is $20 \mathrm{kg}-\mathrm{m}^{2}$ about the diameter. Find the moment of inertia about any tangent.\
Sol. According to the theorem of parallel axes, we have
$$
\begin{aligned} \mathrm{I}=\mathrm{I}_{6}+\mathrm{Ma}^{2}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{MR}^{2} &(\because \mathrm{d}=\mathrm{R}) \\=&\left.\frac{7}{5} \mathrm{MR}^{2}=\frac{7}{2} \times \frac{2}{5} \mathrm{MR}^{2}=\frac{7}{2} \times 20=70 \mathrm{kg}-\mathrm{m}^{2} \quad \text { (Given } \frac{2}{5} \mathrm{MR}^{2}=20\right) \end{aligned}
$$
Ex. If the moment of inertia of a disc about an axis tangentially and parallel to its surface be I, what will be the moment of inertia about the axis tangential but perpendicular to the surface.
Sol. According to the theorem of parallel axes, the moment of inertia of the disc about an axis tangentially
and parallel to the surface is given by-
$$
\mathrm{I}=\mathrm{I}_{\|}=\frac{\mathrm{MR}^{2}}{4}+\mathrm{MR}^{2}=\frac{5}{4} \mathrm{MR}^{2}
$$
The moment of inertia of the disc about an axis tangential but perpendicular to the surface is given by
$$
\mathrm{I}^{\prime}=\frac{\mathrm{MR}^{2}}{2}+\mathrm{MR}^{2}=\frac{3}{2} \mathrm{MR}^{2}=\frac{6}{5}\left[\frac{5}{4} \mathrm{MR}^{2}\right]=\frac{6}{5} \mathrm{I}
$$
Ex. Find the moment of inertia of a uniform semicircular wire of mass $M$ and radius $r$ about a line perpendicular to the plane of the wire through the center.
$\mathrm{I}=\mathrm{I}_{\mathrm{g}}+\mathrm{Md}^{2}$
Ex. The diameter of flywheel increases by $1 \%$. Find the percentage increase in moment of inertia about axis of symmetry.
Sol. The moment of inertia of flywheel is given by, $\quad \mathrm{I}=\mathrm{MR}^{2}$
Taking log, $\quad \log \mathrm{I}=\log \mathrm{M}+2 \log \mathrm{R}$
Differentiating, $\quad \frac{\mathrm{d} \mathrm{I}}{\mathrm{I}}=0+2 \frac{\mathrm{d} \mathrm{R}}{\mathrm{R}}$
$\therefore \quad \%$ change in moment of inertia $=\frac{d I}{I} \times 100=2 \times 1 \%=2 \%$
Ex. The moment of inertia of sphere is $20 \mathrm{kg}-\mathrm{m}^{2}$ about the diameter. Find the moment of inertia about any tangent.\
Sol. According to the theorem of parallel axes, we have
$$
\begin{aligned} \mathrm{I}=\mathrm{I}_{6}+\mathrm{Ma}^{2}=\frac{2}{5} \mathrm{MR}^{2}+\mathrm{MR}^{2} &(\because \mathrm{d}=\mathrm{R}) \\=&\left.\frac{7}{5} \mathrm{MR}^{2}=\frac{7}{2} \times \frac{2}{5} \mathrm{MR}^{2}=\frac{7}{2} \times 20=70 \mathrm{kg}-\mathrm{m}^{2} \quad \text { (Given } \frac{2}{5} \mathrm{MR}^{2}=20\right) \end{aligned}
$$
Ex. If the moment of inertia of a disc about an axis tangentially and parallel to its surface be I, what will be the moment of inertia about the axis tangential but perpendicular to the surface.
Sol. According to the theorem of parallel axes, the moment of inertia of the disc about an axis tangentially
and parallel to the surface is given by-
$$
\mathrm{I}=\mathrm{I}_{\|}=\frac{\mathrm{MR}^{2}}{4}+\mathrm{MR}^{2}=\frac{5}{4} \mathrm{MR}^{2}
$$
The moment of inertia of the disc about an axis tangential but perpendicular to the surface is given by
$$
\mathrm{I}^{\prime}=\frac{\mathrm{MR}^{2}}{2}+\mathrm{MR}^{2}=\frac{3}{2} \mathrm{MR}^{2}=\frac{6}{5}\left[\frac{5}{4} \mathrm{MR}^{2}\right]=\frac{6}{5} \mathrm{I}
$$
Ex. Find the moment of inertia of a uniform semicircular wire of mass $M$ and radius $r$ about a line perpendicular to the plane of the wire through the center.
 $\begin{array}{ll}{\text { Sol. }} & {\delta \mathrm{I}=\delta \mathrm{m} . \mathrm{r}^{2}} \\ {\qquad \begin{aligned} \mathrm{I} &=r^{2} \Sigma \delta \mathrm{m} \\ &=\mathrm{Mr}^{2} \end{aligned}}\end{array}$
Ex. Two uniform, thin identical rods each of mass $M$ and length L are joined so as to form a cross as shown in fig. Find the moment of inertia of the cross about a bisector line AC.
Sol. Moment of inertia of cross about axis passing through $\mathrm{O}$ and perpendicualr to the plane of rods.
$\mathrm{I}_{0}=\frac{\mathrm{ML}^{2}}{12}+\frac{\mathrm{ML}^{2}}{12}$
With the help of theorem of perpendicular axes
$$
\begin{aligned} 2 \mathrm{I}_{\mathrm{AC}}+\mathrm{I}_{\mathrm{BD}}=\mathrm{I}_{0} & \text { c. } \\ \text { or } & \mathrm{I}_{\mathrm{AC}}=\frac{\mathrm{I}_{0}}{2}=\frac{\mathrm{ML}^{2}}{24} &\left(\mathrm{I}_{\mathrm{AC}}=\mathrm{I}_{\mathrm{BD}}\right) \end{aligned}
$$
$\begin{array}{ll}{\text { Sol. }} & {\delta \mathrm{I}=\delta \mathrm{m} . \mathrm{r}^{2}} \\ {\qquad \begin{aligned} \mathrm{I} &=r^{2} \Sigma \delta \mathrm{m} \\ &=\mathrm{Mr}^{2} \end{aligned}}\end{array}$
Ex. Two uniform, thin identical rods each of mass $M$ and length L are joined so as to form a cross as shown in fig. Find the moment of inertia of the cross about a bisector line AC.
Sol. Moment of inertia of cross about axis passing through $\mathrm{O}$ and perpendicualr to the plane of rods.
$\mathrm{I}_{0}=\frac{\mathrm{ML}^{2}}{12}+\frac{\mathrm{ML}^{2}}{12}$
With the help of theorem of perpendicular axes
$$
\begin{aligned} 2 \mathrm{I}_{\mathrm{AC}}+\mathrm{I}_{\mathrm{BD}}=\mathrm{I}_{0} & \text { c. } \\ \text { or } & \mathrm{I}_{\mathrm{AC}}=\frac{\mathrm{I}_{0}}{2}=\frac{\mathrm{ML}^{2}}{24} &\left(\mathrm{I}_{\mathrm{AC}}=\mathrm{I}_{\mathrm{BD}}\right) \end{aligned}
$$
 Introduction to Rotational Dynamics
Moment of Inertia
Moment of Inertia: Perpendicular and Parallel axis theorem
Radius of Gyration
Law of Conservation of Angular Momentum
Conservation of Angular Momentum Examples
Kinetic Energy of a Rotating Body
Work done in rotatory Motion
Rotational Power
Combine Translational and Rotational Motion
Rolling without slipping
Rolling on a plane surface
Rolling on a Inclined Plane
For Latest updates, Subscribe our Youtube Channel
Introduction to Rotational Dynamics
Moment of Inertia
Moment of Inertia: Perpendicular and Parallel axis theorem
Radius of Gyration
Law of Conservation of Angular Momentum
Conservation of Angular Momentum Examples
Kinetic Energy of a Rotating Body
Work done in rotatory Motion
Rotational Power
Combine Translational and Rotational Motion
Rolling without slipping
Rolling on a plane surface
Rolling on a Inclined Plane
For Latest updates, Subscribe our Youtube Channel 