eSaral provides chemistry short notes for JEE and NEET to help students in revising topics quickly. These notes are completely based on latest syllabus and it includes all the tips and tricks that will help you in learning chemistry better and score well.
The Notes will help you to understand the important topics and remember the key points for exam point of view.
You can also access detailed Notes of chemistry here.
Download or View Detailed Notes for Chemistry Class 11th
Download or View Detailed Notes for Chemistry Class 12th
Ionic Equilibrium
Theory
Fundamentals of Acids, Bases & Ionic Equilibrium
Acids & Bases
When dissolved in water, acids release $\mathrm{H}^{+}$ ions, base release $\mathrm{OH}^{-}$ ions.
Arrhenius Theory
When dissolved in water, the substances which release
(i) $\mathrm{H}^{+}$ ions are called acids (ii) $\mathrm{OH}^{-}$ ions are called bases
Bronsted & Lowry Concept
Acids are proton donors, bases are proton acceptors
Note that as per this definition, water is not necessarily the solvent.
When a substance is dissolved in water, it is said to react with water e.g.
$\mathrm{HCl}+\mathrm{H}_{2} \mathrm{O} \rightarrow \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{Cl}^{-}$ ; HCl donates H+ to water, hence acid.
$\mathrm{NH}_{3}+\mathrm{H}_{2} \mathrm{O} \quad \rightarrow \mathrm{NH}_{4}^{+}+\mathrm{OH}^{-}$ ; NH3 takes H+ from water, hence base.
For the backward reaction, $N H_{4}^{+}$ donate $H^{+}$ , hence it is an acid; $O H^{-}$ accepts H+, hence it is base. $N H_{3}$ (base) & $N H_{4}^{+}$ (acid) from conjugate acid base pair.
Conjugate acid and bases
To get conjugate acid of a given species add $\mathrm{H}^{+}$ to it. e.g. conjugate acid of N2H4 is N2H5+.
To get conjugate base of any species subtract H+ from it. e.g. Conjugate base of $\mathrm{NH}_{3}$ is $\mathrm{NH}_{2}^{-}$.
Note: Although $C I^{-}$ is conjugate base of HCl, it is not a base as an independent species. In fact,anions of all strong acid like $C I, N O_{3}^{-}, C l O_{4}^{-}$ etc. are neutral anions. Same is true for cations of strong bases like $K^{+}, N a^{+}, B a^{++}$ etc. When they are dissolved in water, they do not react with water (i.e. they do not undergo hydrolysis) and these ions do not cause any change in pH of water (others like $\left.C N^{-} d o\right)$.
Some examples of :
Basic Anions : $\mathrm{CH}_{3} \mathrm{COO}^{-}, \mathrm{OH}^{-}, \mathrm{CN}^{-}$ (Conjugate bases of weak acids)
Acid Anions: $H S O_{3}^{-}, H S^{-}$ etc. Note that these ions are amphoteric, i.e. they can behave both as an acid and as a base. e.g. for $\mathrm{H}_{2} \mathrm{PO}_{4}^{-}:$
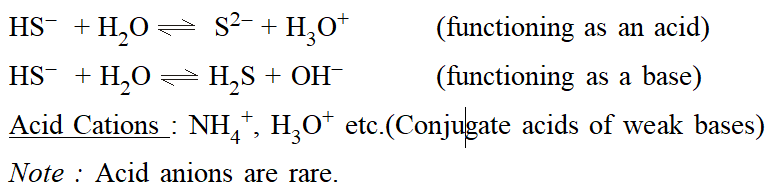Lewis Concept : Acids are substances which accept a pair of electrons to form a coordinate bond and bases are the substances which donate a pair of electrons to form a coordinate bond.
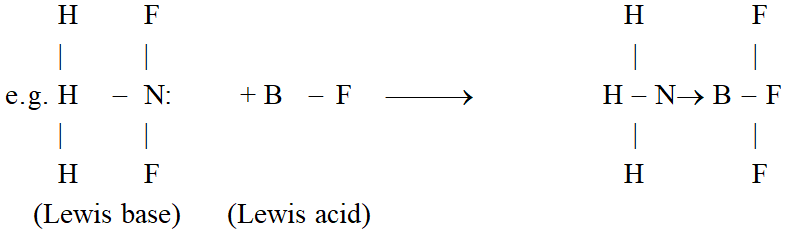Important : $\mathrm{Ca}+\mathrm{S} \rightarrow \mathrm{Ca}^{2+}+\mathrm{S}^{2-}$ is not a Lewis acidbase reaction since dative bond is not formed.
Lewis Acids : As per Lewis concept, following species can acts as Lewis Acids :
(i) Molecules in which central atom has incomplete octet. \text { (e.g. }\left.\mathrm{BF}_{3}, \mathrm{AlCl}_{3} \text { etc. }\right)
(ii) Molecules which have a central atom with empty d orbitals \text { (e.g. }\left.\operatorname{six}_{4}, \mathrm{GeX}_{4}, \mathrm{PX}_{3}, \mathrm{TiCl}_{4} \text { etc. }\right)
(iii) Simple Cations: Though all cations can be expected to be Lewis acids, \mathrm{Na}^{+}, \mathrm{Ca}^{++}, \mathrm{K}^{+} \text {etc. } show no tendency to accept electrons. However \mathrm{H}^{+}, \mathrm{Ag}^{+} etc. act as Lewis acids.
(iv) Molecules having multiple bond between atoms of dissimilar electronegativity.
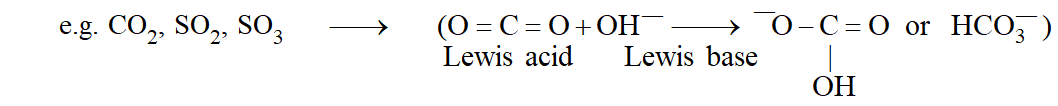Lewis bases are typically :
(i) Neutral species having at least one lone pair of electrons.
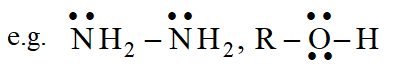
Autoprotolysis of water (or any solvent)
\text { Autoprotolysis (or self-ionization) constant }\left(\mathrm{K}_{\mathrm{w}}\right)=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]
\text { Hence, } \mathrm{pH}+\mathrm{pOH}=\mathrm{pK}_{\mathrm{w}} \text { at all temperatures }
Condition of neutrality \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right] \text {(for water as solvent) }
\text { At } 25^{\circ} \mathrm{C}, \mathrm{K}_{\mathrm{W}}=10^{-14} \cdot \mathrm{K}_{\mathrm{W}}
increases with increase in temperature. Accordingly, the neutral
point of water \left(\mathrm{pH}=7 \text { at } 25^{\circ} \mathrm{C}\right) also shifts to a value lower than 7 with increase in temperature.
Important: \mathrm{K}_{\mathrm{W}}=10^{-14} s a value at \text { (i) } 25^{\circ} \mathrm{C} \text { (ii) }for water only. If the temperature changes or if some other solvent is used, autoprotolysis constant will not be same.
Ionisation Constant
* \quad \text { For dissociation of weak acids (eg. HCN), HCN + H_{ } 2 } \mathrm{O} \text { 1 } \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{CN}^{-} \text {the equilibrium }
constant expression is written as Ka =\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{CN}^{-}\right]}{[\mathrm{HCN}]}
* For the Polyprotic acids \left(\mathrm{e} \cdot \mathrm{g} \cdot \mathrm{H}_{3} \mathrm{PO}_{4}\right) sucessive ionisation constants are denoted \text { by } \mathrm{K}_{1}, \mathrm{K}_{2}, \mathrm{K}_{3} \text { etc. } For \mathrm{H}_{3} \mathrm{PO}_{4},
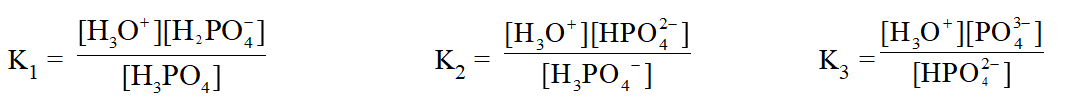\text { Similarly, } \mathrm{K}_{\mathrm{b}} \text { denotes basic dissociation constant for a base. }
\text { Also, } \mathrm{pK}_{\mathrm{a}}=-\log _{10} \mathrm{K}_{\mathrm{a}}, \mathrm{pK}_{\mathrm{b}}=-\log _{10} \mathrm{K}_{\mathrm{b}}
\text { Some Important Results: }\left[\mathrm{H}^{+}\right] \text {concentration of }
Case (i) A weak acid in water
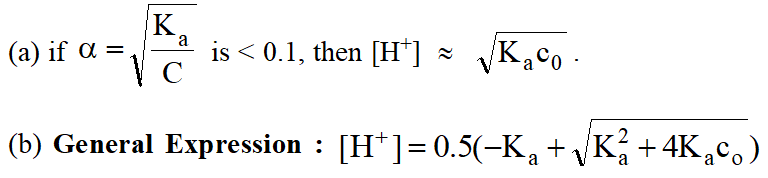Similarly for a weak base, substitute \left[\mathrm{OH}^{-}\right] \text {and } \mathrm{K}_{\mathrm{b}} instead of \left[\mathrm{H}^{+}\right] \text {and } \mathrm{K}_{\mathrm{a}}
respectively in these expressions.
Case (ii) (a) A weak acid and a strong acid \left[\mathrm{H}^{+}\right] is entirely due to dissociation of strong acid
(b) A weak base and a strong base \left[\mathrm{H}^{+}\right] is entirely due to dissociation of strong base
Neglect the contribution of weak acid/base usually.
Condition for neglecting : \text { If } \mathrm{c}_{0} concentration of strong acid, c_{1} = concentration of
weak acid then neglect the contribution of weak acid if \mathrm{K}_{\mathrm{a}} \leq 0.01 \mathrm{c}_{0}^{2 /} \mathrm{c}_{1}
Case (iii) Two (or more) weak acids
Proceed by the general method of applying two conditions
(i) of electroneutrality (ii) of equilibria.
The accurate treatement yields a cubic equation. Assuming that acids dissociate to
\text { a negligible extent }\left[\text { i.e. } c_{0}-x \approx c_{0}\right] \quad\left[\mathrm{H}^{+}\right]=\left(\mathrm{K}_{1} \mathrm{c}_{1}+\mathrm{K}_{2} \mathrm{c}_{2}+\ldots+\mathrm{K}_{\mathrm{w}}\right)^{1 / 2}
Case (iv) When dissociation of water becomes significant:
\text { Dissociation of water contributes significantly to }\left[\mathrm{H}^{+}\right] \text {or }\left[\mathrm{OH}^{-}\right] \text {only when for }
(i) strong acids (or bases) : 10^{-8} \mathrm{M}<\mathrm{c}_{0}<10^{-6} \mathrm{M}. Neglecting ionisation of water at
10^{-6} \mathrm{M} \text { causes } 1 \% \text { error (approvable). Below } 10^{-8} \mathrm{M}, Neglecting ionisation of water at 10^{-6} \mathrm{M} \text { causes } 1 \% \text { error (approvable). } Below 10^{-8} \mathrm{M}, contribution of acid (or base) can be neglected and pH can be taken to be practically 7.
Weak acids (or bases) : \text { When } \mathrm{K}_{\mathrm{a}} \mathrm{c}_{0}<10^{-12}
then consider dissociation of water as well.
HYDROLYSIS
* Salts of strong acids and strong bases do not undergo hydrolysis.
* Salts of a strong acids and weak bases give an acidic solution. e.g. \mathrm{NH}_{4} \mathrm{Cl} when
dissolved, it dissociates to give \mathrm{NH}_{4}^{+} ions and \mathrm{NH}_{4}^{+}+\mathrm{H}_{2} \mathrm{O} \quad 1 \quad \mathrm{NH}_{3}+\mathrm{H}_{3} \mathrm{O}^{+}
\mathrm{K}_{\mathrm{h}}=\left[\mathrm{NH}_{3}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] /\left[\mathrm{NH}_{4}^{+}\right]=\mathrm{K}_{\mathrm{W}} / \mathrm{K}_{\mathrm{b}} of conjugate base of \mathrm{NH}_{4}^{+}
Important! In general : \mathrm{K}_{\mathrm{a}}(\text { of an acid }) \mathrm{xK}_{\mathrm{b}} \text { (of its conjugate base) }=\mathrm{K}_{\mathrm{w}}
If the degree of hydrolysis(h) is small (<<1), \quad \mathrm{h}=\sqrt{\mathrm{K}_{\mathrm{h}} \mathrm{c}_{0}}
Otherwise h = \frac{-\mathrm{K}_{\mathrm{h}}+\sqrt{\mathrm{K}_{\mathrm{h}}^{2}+4 \mathrm{K}_{\mathrm{h}} \mathrm{c}_{0}}}{2 \mathrm{c}_{0}}, \quad\left[\mathrm{H}^{+}\right]=\mathrm{c}_{0} \mathrm{h}
* Salts of strong base and weak acid give a basic solution (\mathrm{pH}>7) when dissolved in water, e.g. NaCN,
\mathrm{CN}^{-}+\mathrm{H}_{2} \mathrm{O} \quad 1 \quad \mathrm{HCN}+\mathrm{OH}^{-} \quad\left[\mathrm{OH}^{-}\right]=\mathrm{c}_{0} \mathrm{h}, \mathrm{h}=\sqrt{\mathrm{K}_{\mathrm{h}} \mathrm{c}_{0}}
* Salts of weak base and weak acid
Assuming degree of hydrolysis to be same for the both the ions,
\mathrm{K}_{\mathrm{h}}=\mathrm{K}_{\mathrm{w}} /\left(\mathrm{K}_{\mathrm{a}} \cdot \mathrm{K}_{\mathrm{b}}\right),\left[\mathrm{H}^{+}\right]=\left[\mathrm{K}_{\mathrm{a}} \mathrm{K}_{\mathrm{w}} / \mathrm{K}_{\mathrm{b}}\right]^{1 / 2}
Note: Exact treatment of this case is difficult to solve. So use this assumption in general cases.
Also, degree of anion or cation will be much higher in the case of a salt of weak acid and weak base. This is because each of them gets hydrolysed, producing \mathrm{H}^{+} \text {and } \mathrm{OH}^{-} ions. These ions combine to form water and the hydrolysis equilibrium is shifted in the forward direaction.
Buffer Solutions are the solutions whose pH does not change significantly on adding a small quantity of strong base or on little dilution.
These are typically made by mixing a weak acid (or base) with its conjugate base (or acid). e.g. \mathrm{CH}_{3} \mathrm{COOH} with \mathrm{CH}_{3} \mathrm{COONa}, \mathrm{NH}_{3}(\mathrm{aq}) \text { with } \mathrm{NH}_{4} \mathrm{Cl} \text { etc. }
\text { If }\left.\mathrm{K}_{\mathrm{a}} \text { for acid (or } \mathrm{K}_{\mathrm{b}} \text { for base }\right) (or Kb for base) is not too high, we may write :
Henderson's Equation
\mathrm{pH}=\mathrm{pK}_{\mathrm{a}}+\log \{[\mathrm{salt}] /[\mathrm{acid}]\} for weak acid with its conjugate base.
\text { or } \mathrm{pOH}=\mathrm{pK}_{\mathrm{b}}+\log \{[\mathrm{salt}] /[\text { base }]\} for weak base with its conjugate acid.
Important : For good buffer capacity, [salt] : [acid ratios should be as close to one as possible. In such a case, \mathrm{pH}=\mathrm{pK}_{\mathrm{a}} (This also is the case at midpoint of titration)
Buffer capacity = (no. of moles of acid (or base) added to 1L) / (change in pH)
Indicators. Indicator is a substance which indicates the point of equivalence in a titration by undergoing a change in its colour. They are weak acids or weak bases.
Theory of Indicators. The ionized and unionized forms of indicators have different colours. If 90 % or more of a particular form (ionised or unionised) is present, then its colour can be distinclty seen.In general, for an indicator which is weak acid, HIn l H+ + In–, the ratio of ionized to unionized form can be determined from
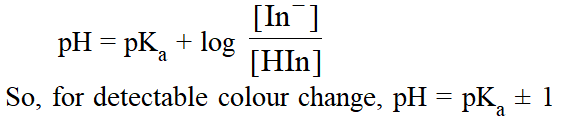This roughly gives the range of indicators. Ranges for some popular indicators are
Table 1 : Indicators
Equivalence point. The point at which exactly equivalent amounts of acid and base have been mixed.
Acid Base Titration. For choosing a suitable indicator titration curves are of great help. In a titration curve, change in pH is plotted against the volume of alkali to a given acid. Four cases arise.
(a) Strong acid vs strong base. The curve is almost vertical over the pH range 3.5-10. This abrupt change corresponds to equivalence point. Any indicator suitable.
(b) Weak acid vs strong base. Final solution is basic 9 at equivalence point. Vertical region (not so sharp) lies in pH range 6.5-10. So, phenolphathlene is suitable.
(c) Strong acid vs weak base. Final solution acidic. Vertical point in pH range 3.8-7.2. Methyl red or methyl orange suitable.
(d) Weak acid vs weak base. No sharp change in pH. No suitable indicator.
Note : at midpoint of titration, \mathrm{pH}=\mathrm{pK}_{\mathrm{a}}, thus by pH measurements, Ka for weak acids (or K_{b} for weak bases) can be determined.
Polyprotic acids and bases. \text { Usually } \mathrm{K}_{2}, \mathrm{K}_{3} \text { etc. can be safely neglected and only } \mathrm{K}_{1} \text { plays a significant }
Solubility product \left(\mathbf{K}_{\mathbf{s p}}\right). For sparingly soluble salts (eg. \mathrm{Ag}_{2} \mathrm{C}_{2} \mathrm{O}_{4}) an equilibrium which exists is
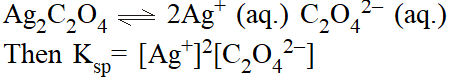Precipitation. Whenever the product of concentrations (raised to appropriate power) exceeds the solubility product, precipitation occurs.
Common ion effects. Suppression of dissociation by adding an ion common with dissociation products. \text { e.g. } \mathrm{Ag}^{+} \text {or } \mathrm{C}_{2} \mathrm{O}_{4}^{2-} in the above example.
Simultaneous solubility. While solving these problems, go as per general method i.e.
(i) First apply condition of electroneutrality and
(ii) Apply the equilibria conditions.
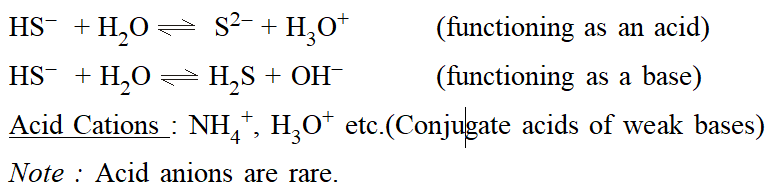Lewis Concept : Acids are substances which accept a pair of electrons to form a coordinate bond and bases are the substances which donate a pair of electrons to form a coordinate bond.
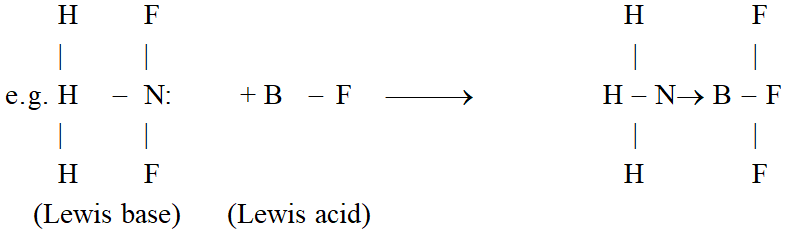Important : $\mathrm{Ca}+\mathrm{S} \rightarrow \mathrm{Ca}^{2+}+\mathrm{S}^{2-}$ is not a Lewis acidbase reaction since dative bond is not formed.
Lewis Acids : As per Lewis concept, following species can acts as Lewis Acids :
(i) Molecules in which central atom has incomplete octet. \text { (e.g. }\left.\mathrm{BF}_{3}, \mathrm{AlCl}_{3} \text { etc. }\right)
(ii) Molecules which have a central atom with empty d orbitals \text { (e.g. }\left.\operatorname{six}_{4}, \mathrm{GeX}_{4}, \mathrm{PX}_{3}, \mathrm{TiCl}_{4} \text { etc. }\right)
(iii) Simple Cations: Though all cations can be expected to be Lewis acids, \mathrm{Na}^{+}, \mathrm{Ca}^{++}, \mathrm{K}^{+} \text {etc. } show no tendency to accept electrons. However \mathrm{H}^{+}, \mathrm{Ag}^{+} etc. act as Lewis acids.
(iv) Molecules having multiple bond between atoms of dissimilar electronegativity.
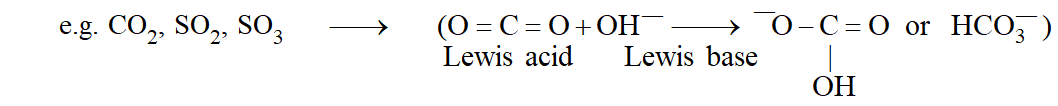Lewis bases are typically :
(i) Neutral species having at least one lone pair of electrons.
Autoprotolysis of water (or any solvent)
\text { Autoprotolysis (or self-ionization) constant }\left(\mathrm{K}_{\mathrm{w}}\right)=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]
\text { Hence, } \mathrm{pH}+\mathrm{pOH}=\mathrm{pK}_{\mathrm{w}} \text { at all temperatures }
Condition of neutrality \left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right] \text {(for water as solvent) }
\text { At } 25^{\circ} \mathrm{C}, \mathrm{K}_{\mathrm{W}}=10^{-14} \cdot \mathrm{K}_{\mathrm{W}}
increases with increase in temperature. Accordingly, the neutral
point of water \left(\mathrm{pH}=7 \text { at } 25^{\circ} \mathrm{C}\right) also shifts to a value lower than 7 with increase in temperature.
Important: \mathrm{K}_{\mathrm{W}}=10^{-14} s a value at \text { (i) } 25^{\circ} \mathrm{C} \text { (ii) }for water only. If the temperature changes or if some other solvent is used, autoprotolysis constant will not be same.
Ionisation Constant
* \quad \text { For dissociation of weak acids (eg. HCN), HCN + H_{ } 2 } \mathrm{O} \text { 1 } \mathrm{H}_{3} \mathrm{O}^{+}+\mathrm{CN}^{-} \text {the equilibrium }
constant expression is written as Ka =\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{CN}^{-}\right]}{[\mathrm{HCN}]}
* For the Polyprotic acids \left(\mathrm{e} \cdot \mathrm{g} \cdot \mathrm{H}_{3} \mathrm{PO}_{4}\right) sucessive ionisation constants are denoted \text { by } \mathrm{K}_{1}, \mathrm{K}_{2}, \mathrm{K}_{3} \text { etc. } For \mathrm{H}_{3} \mathrm{PO}_{4},
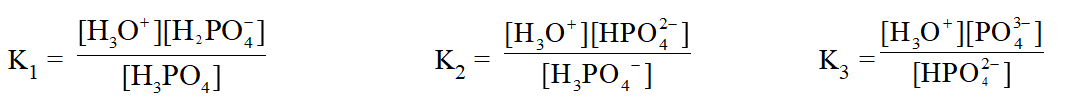\text { Similarly, } \mathrm{K}_{\mathrm{b}} \text { denotes basic dissociation constant for a base. }
\text { Also, } \mathrm{pK}_{\mathrm{a}}=-\log _{10} \mathrm{K}_{\mathrm{a}}, \mathrm{pK}_{\mathrm{b}}=-\log _{10} \mathrm{K}_{\mathrm{b}}
\text { Some Important Results: }\left[\mathrm{H}^{+}\right] \text {concentration of }
Case (i) A weak acid in water
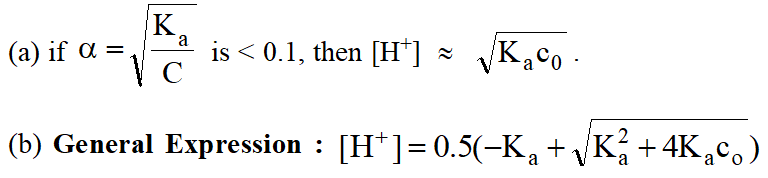Similarly for a weak base, substitute \left[\mathrm{OH}^{-}\right] \text {and } \mathrm{K}_{\mathrm{b}} instead of \left[\mathrm{H}^{+}\right] \text {and } \mathrm{K}_{\mathrm{a}}
respectively in these expressions.
Case (ii) (a) A weak acid and a strong acid \left[\mathrm{H}^{+}\right] is entirely due to dissociation of strong acid
(b) A weak base and a strong base \left[\mathrm{H}^{+}\right] is entirely due to dissociation of strong base
Neglect the contribution of weak acid/base usually.
Condition for neglecting : \text { If } \mathrm{c}_{0} concentration of strong acid, c_{1} = concentration of
weak acid then neglect the contribution of weak acid if \mathrm{K}_{\mathrm{a}} \leq 0.01 \mathrm{c}_{0}^{2 /} \mathrm{c}_{1}
Case (iii) Two (or more) weak acids
Proceed by the general method of applying two conditions
(i) of electroneutrality (ii) of equilibria.
The accurate treatement yields a cubic equation. Assuming that acids dissociate to
\text { a negligible extent }\left[\text { i.e. } c_{0}-x \approx c_{0}\right] \quad\left[\mathrm{H}^{+}\right]=\left(\mathrm{K}_{1} \mathrm{c}_{1}+\mathrm{K}_{2} \mathrm{c}_{2}+\ldots+\mathrm{K}_{\mathrm{w}}\right)^{1 / 2}
Case (iv) When dissociation of water becomes significant:
\text { Dissociation of water contributes significantly to }\left[\mathrm{H}^{+}\right] \text {or }\left[\mathrm{OH}^{-}\right] \text {only when for }
(i) strong acids (or bases) : 10^{-8} \mathrm{M}<\mathrm{c}_{0}<10^{-6} \mathrm{M}. Neglecting ionisation of water at
10^{-6} \mathrm{M} \text { causes } 1 \% \text { error (approvable). Below } 10^{-8} \mathrm{M}, Neglecting ionisation of water at 10^{-6} \mathrm{M} \text { causes } 1 \% \text { error (approvable). } Below 10^{-8} \mathrm{M}, contribution of acid (or base) can be neglected and pH can be taken to be practically 7.
Weak acids (or bases) : \text { When } \mathrm{K}_{\mathrm{a}} \mathrm{c}_{0}<10^{-12}
then consider dissociation of water as well.
HYDROLYSIS
* Salts of strong acids and strong bases do not undergo hydrolysis.
* Salts of a strong acids and weak bases give an acidic solution. e.g. \mathrm{NH}_{4} \mathrm{Cl} when
dissolved, it dissociates to give \mathrm{NH}_{4}^{+} ions and \mathrm{NH}_{4}^{+}+\mathrm{H}_{2} \mathrm{O} \quad 1 \quad \mathrm{NH}_{3}+\mathrm{H}_{3} \mathrm{O}^{+}
\mathrm{K}_{\mathrm{h}}=\left[\mathrm{NH}_{3}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] /\left[\mathrm{NH}_{4}^{+}\right]=\mathrm{K}_{\mathrm{W}} / \mathrm{K}_{\mathrm{b}} of conjugate base of \mathrm{NH}_{4}^{+}
Important! In general : \mathrm{K}_{\mathrm{a}}(\text { of an acid }) \mathrm{xK}_{\mathrm{b}} \text { (of its conjugate base) }=\mathrm{K}_{\mathrm{w}}
If the degree of hydrolysis(h) is small (<<1), \quad \mathrm{h}=\sqrt{\mathrm{K}_{\mathrm{h}} \mathrm{c}_{0}}
Otherwise h = \frac{-\mathrm{K}_{\mathrm{h}}+\sqrt{\mathrm{K}_{\mathrm{h}}^{2}+4 \mathrm{K}_{\mathrm{h}} \mathrm{c}_{0}}}{2 \mathrm{c}_{0}}, \quad\left[\mathrm{H}^{+}\right]=\mathrm{c}_{0} \mathrm{h}
* Salts of strong base and weak acid give a basic solution (\mathrm{pH}>7) when dissolved in water, e.g. NaCN,
\mathrm{CN}^{-}+\mathrm{H}_{2} \mathrm{O} \quad 1 \quad \mathrm{HCN}+\mathrm{OH}^{-} \quad\left[\mathrm{OH}^{-}\right]=\mathrm{c}_{0} \mathrm{h}, \mathrm{h}=\sqrt{\mathrm{K}_{\mathrm{h}} \mathrm{c}_{0}}
* Salts of weak base and weak acid
Assuming degree of hydrolysis to be same for the both the ions,
\mathrm{K}_{\mathrm{h}}=\mathrm{K}_{\mathrm{w}} /\left(\mathrm{K}_{\mathrm{a}} \cdot \mathrm{K}_{\mathrm{b}}\right),\left[\mathrm{H}^{+}\right]=\left[\mathrm{K}_{\mathrm{a}} \mathrm{K}_{\mathrm{w}} / \mathrm{K}_{\mathrm{b}}\right]^{1 / 2}
Note: Exact treatment of this case is difficult to solve. So use this assumption in general cases.
Also, degree of anion or cation will be much higher in the case of a salt of weak acid and weak base. This is because each of them gets hydrolysed, producing \mathrm{H}^{+} \text {and } \mathrm{OH}^{-} ions. These ions combine to form water and the hydrolysis equilibrium is shifted in the forward direaction.
Buffer Solutions are the solutions whose pH does not change significantly on adding a small quantity of strong base or on little dilution.
These are typically made by mixing a weak acid (or base) with its conjugate base (or acid). e.g. \mathrm{CH}_{3} \mathrm{COOH} with \mathrm{CH}_{3} \mathrm{COONa}, \mathrm{NH}_{3}(\mathrm{aq}) \text { with } \mathrm{NH}_{4} \mathrm{Cl} \text { etc. }
\text { If }\left.\mathrm{K}_{\mathrm{a}} \text { for acid (or } \mathrm{K}_{\mathrm{b}} \text { for base }\right) (or Kb for base) is not too high, we may write :
Henderson's Equation
\mathrm{pH}=\mathrm{pK}_{\mathrm{a}}+\log \{[\mathrm{salt}] /[\mathrm{acid}]\} for weak acid with its conjugate base.
\text { or } \mathrm{pOH}=\mathrm{pK}_{\mathrm{b}}+\log \{[\mathrm{salt}] /[\text { base }]\} for weak base with its conjugate acid.
Important : For good buffer capacity, [salt] : [acid ratios should be as close to one as possible. In such a case, \mathrm{pH}=\mathrm{pK}_{\mathrm{a}} (This also is the case at midpoint of titration)
Buffer capacity = (no. of moles of acid (or base) added to 1L) / (change in pH)
Indicators. Indicator is a substance which indicates the point of equivalence in a titration by undergoing a change in its colour. They are weak acids or weak bases.
Theory of Indicators. The ionized and unionized forms of indicators have different colours. If 90 % or more of a particular form (ionised or unionised) is present, then its colour can be distinclty seen.In general, for an indicator which is weak acid, HIn l H+ + In–, the ratio of ionized to unionized form can be determined from
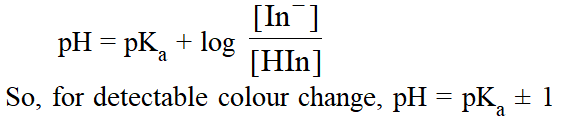This roughly gives the range of indicators. Ranges for some popular indicators are
Table 1 : Indicators
Equivalence point. The point at which exactly equivalent amounts of acid and base have been mixed.
Acid Base Titration. For choosing a suitable indicator titration curves are of great help. In a titration curve, change in pH is plotted against the volume of alkali to a given acid. Four cases arise.
(a) Strong acid vs strong base. The curve is almost vertical over the pH range 3.5-10. This abrupt change corresponds to equivalence point. Any indicator suitable.
(b) Weak acid vs strong base. Final solution is basic 9 at equivalence point. Vertical region (not so sharp) lies in pH range 6.5-10. So, phenolphathlene is suitable.
(c) Strong acid vs weak base. Final solution acidic. Vertical point in pH range 3.8-7.2. Methyl red or methyl orange suitable.
(d) Weak acid vs weak base. No sharp change in pH. No suitable indicator.
Note : at midpoint of titration, \mathrm{pH}=\mathrm{pK}_{\mathrm{a}}, thus by pH measurements, Ka for weak acids (or K_{b} for weak bases) can be determined.
Polyprotic acids and bases. \text { Usually } \mathrm{K}_{2}, \mathrm{K}_{3} \text { etc. can be safely neglected and only } \mathrm{K}_{1} \text { plays a significant }
Solubility product \left(\mathbf{K}_{\mathbf{s p}}\right). For sparingly soluble salts (eg. \mathrm{Ag}_{2} \mathrm{C}_{2} \mathrm{O}_{4}) an equilibrium which exists is
Precipitation. Whenever the product of concentrations (raised to appropriate power) exceeds the solubility product, precipitation occurs.
Common ion effects. Suppression of dissociation by adding an ion common with dissociation products. \text { e.g. } \mathrm{Ag}^{+} \text {or } \mathrm{C}_{2} \mathrm{O}_{4}^{2-} in the above example.
Simultaneous solubility. While solving these problems, go as per general method i.e.
(i) First apply condition of electroneutrality and
(ii) Apply the equilibria conditions.