NCERT Solutions for Class 9 Maths chapter 6 Exercise 6.3

Download now India's Best Exam Prepration App Class 8-9-10, JEE & NEET
Video Lectures	Live Sessions
Study Material	Tests
Previous Year Paper	Revision

Download now India's Best Exam Prepration App

Class 8-9-10, JEE & NEET

Video Lectures

Live Sessions

Study Material

Tests

Previous Year Paper

Revision

Hey, are you a class 9 Student and Looking for Ways to Download NCERT Solutions for Class 9 Maths chapter 6 Exercise 6.3? If Yes then you are at the right place.

Here we have listed Class 9 maths chapter 6 exercise 6.3 solutions in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to score high in your class 9 Maths Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.

In this article, we have listed NCERT Solutions for Class 9 Maths chapter 6 Exercise 6.3 that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

India's Best Exam Preparation for Class 9th - Download Now

Download The PDF of NCERT Solutions for Class 9 Maths chapter 6 Exercise 6.3 "Lines and Angles"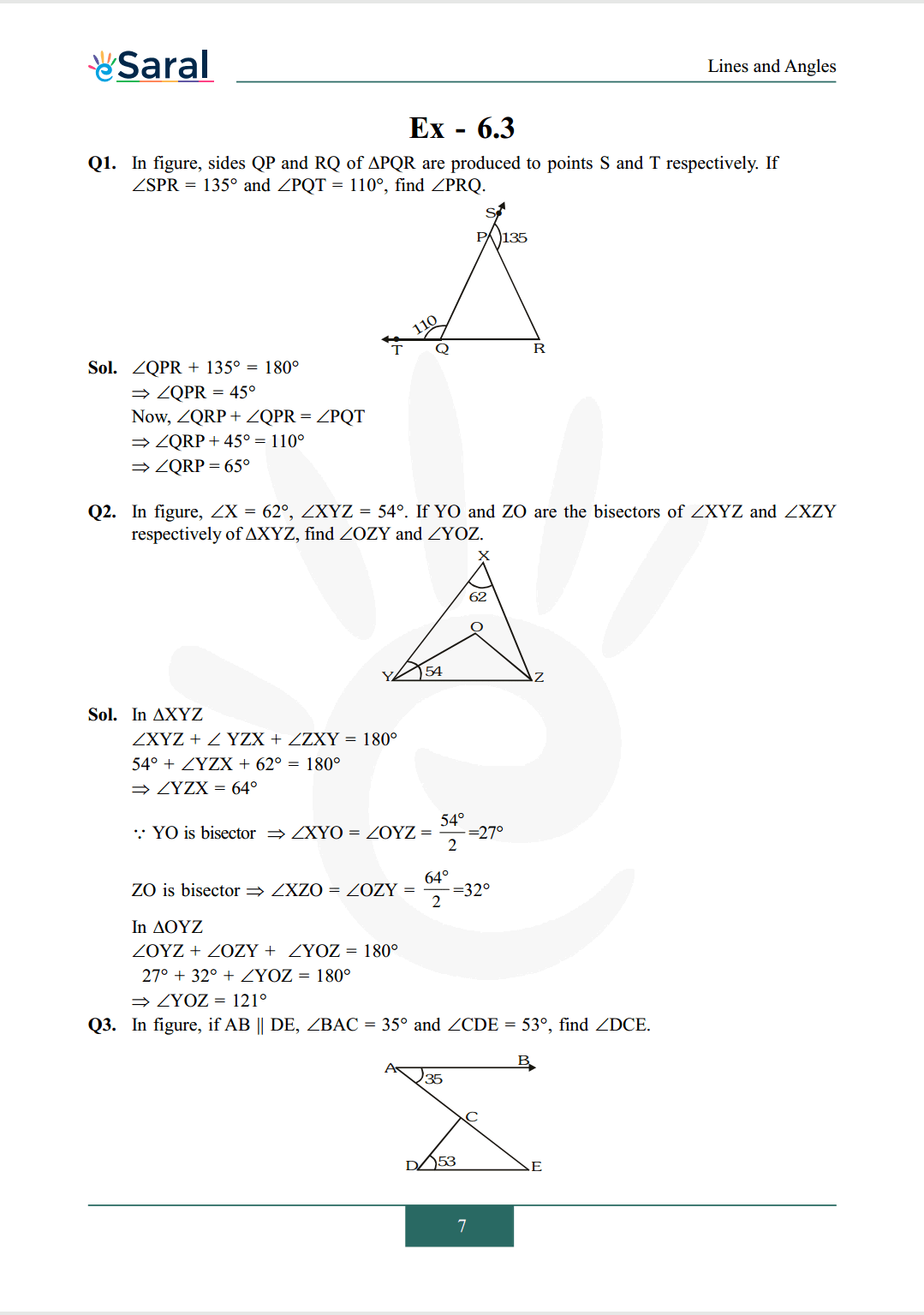

Class 9 maths chapter 6 exercise 6.3 solutions Image 2

So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.

India's Best Exam Preparation for Class 9th - Download Now

All Questions of Chapter 6 Exercise 6.3

Once you complete the chapter 6 then you can revise Ex. 6.3 by solving following questions

Q1. In figure, sides $\mathrm{QP}$ and $\mathrm{RQ}$ of $\Delta \mathrm{PQR}$ are produced to points $\mathrm{S}$ and $\mathrm{T}$ respectively. If $\angle \mathrm{SPR}=135^{\circ}$ and $\angle \mathrm{PQT}=110^{\circ}$, find $\angle \mathrm{PRQ}$.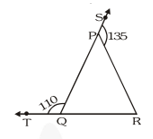

Q2. In figure, $\angle \mathrm{X}=62^{\circ}, \angle \mathrm{XYZ}=54^{\circ}$. If $\mathrm{YO}$ and $\mathrm{ZO}$ are the bisectors of $\angle \mathrm{XYZ}$ and $\angle \mathrm{XZY}$ respectively of $\Delta \mathrm{XYZ}$, find $\angle \mathrm{OZY}$ and $\angle \mathrm{YOZ}$.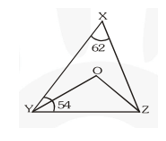

Q3. In figure, if $\mathrm{AB} \| \mathrm{DE}, \angle \mathrm{BAC}=35^{\circ}$ and $\angle \mathrm{CDE}=53^{\circ}$, find $\angle \mathrm{DCE}$.

Q4. In figure, if lines $\mathrm{PQ}$ and RS intersect at point $\mathrm{T}$, such that $\angle \mathrm{PRT}=40^{\circ}, \angle \mathrm{RPT}=95^{-}$ and $\angle \mathrm{TSQ}=75^{\circ}$, find $\angle \mathrm{SQT}$.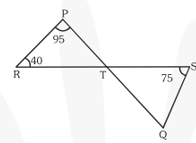

Q5. In figure, if $\mathrm{PQ} \perp \mathrm{PS}, \mathrm{PQ} \| \mathrm{SR}, \angle \mathrm{SQR}=28^{\circ}$ and $\angle \mathrm{QRT}=65^{\circ}$, then find the value of $\mathrm{x}$ and $\mathrm{y}$.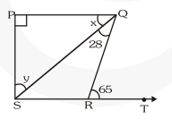

Q6. In figure, the side $\mathrm{QR}$ of $\Delta \mathrm{PQR}$ is produced to a point $\mathrm{S}$. If the bisectors of $\angle \mathrm{PQR}$ and $\angle \mathrm{PRS}$ meet at point $\mathrm{T}$, then prove that $\angle \mathrm{QTR}=\frac{1}{2} \angle \mathrm{QPR}$.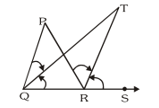

Also Read,