
Hey, are you a class 9 Student and Looking for Ways to Download NCERT Solutions for Class 9 Maths chapter 7 Exercise 7.2? If Yes then you are at the right place.
Here we have listed Class 9 maths chapter 7 exercise 7.2 solutions in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to score high in your class 9 Maths Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solutions for Class 9 Maths chapter 7 Exercise 7.2 that you can download to start your preparations anytime.
So, without wasting more time Let’s start.Download The PDF of NCERT Solutions for Class 9 Maths chapter 7 Exercise 7.2 "Triangles"


So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.
Q1. In an isosceles triangle $\mathrm{ABC}$, with $\mathrm{AB}=\mathrm{AC}$, the bisectors of $\angle \mathrm{B}$ and $\angle \mathrm{C}$ intersect each other at $\mathrm{O}$. Join $\mathrm{A}$ to $\mathrm{O}$. Show that : (i) $\mathrm{OB}=\mathrm{OC}$ (ii) AO bisects $\angle \mathrm{A}$.
Q2. In $\triangle \mathrm{ABC}, \mathrm{AD}$ is the perpendicular bisector of $\mathrm{BC}$. Show that $\triangle \mathrm{ABC}$ is an isosceles triangle in which $\mathrm{AB}=\mathrm{AC}$.

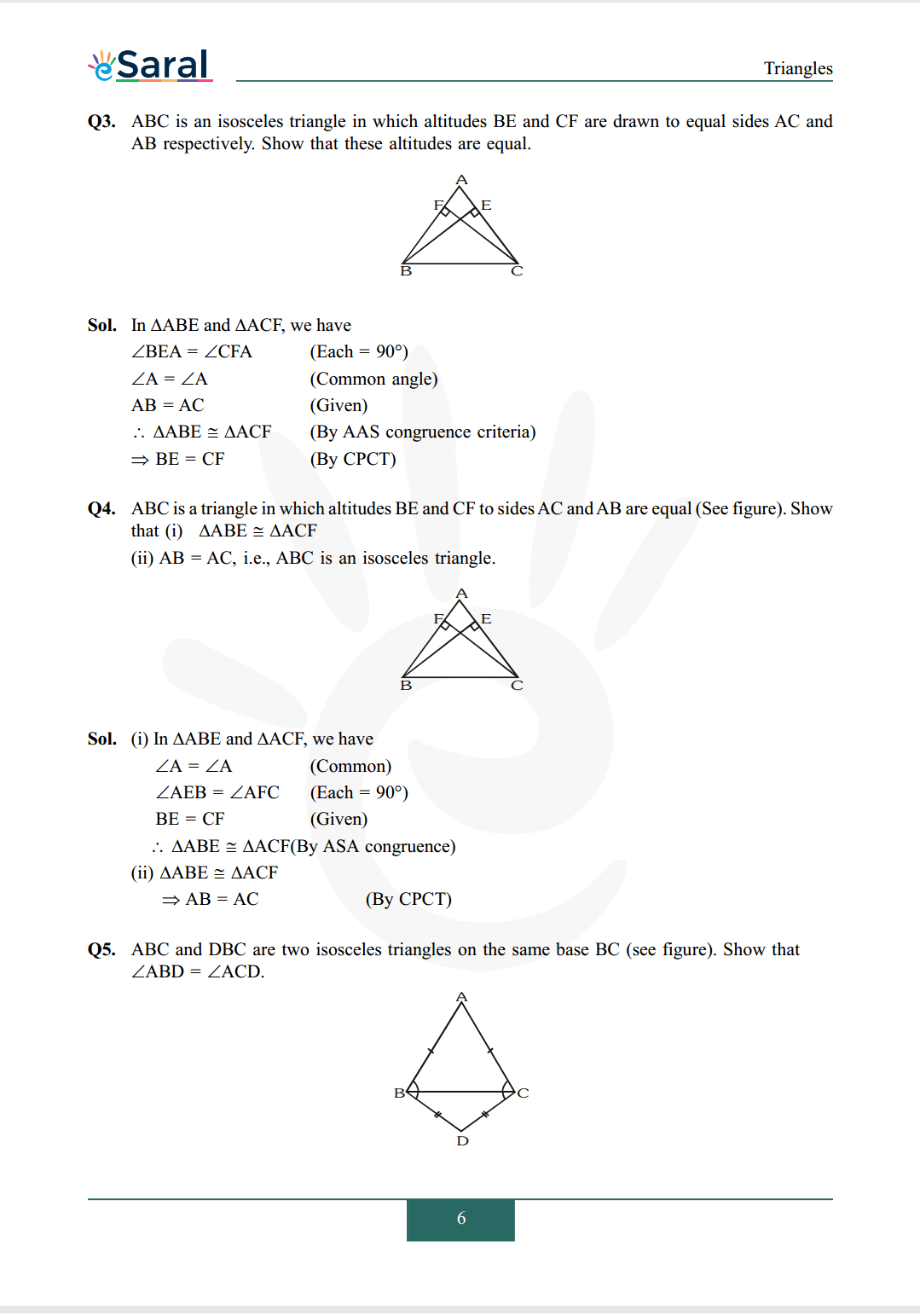
Q3. $\mathrm{ABC}$ is an isosceles triangle in which altitudes $\mathrm{BE}$ and $\mathrm{CF}$ are drawn to equal sides $\mathrm{AC}$ and $\mathrm{AB}$ respectively. Show that these altitudes are equal.

Q4. $\mathrm{ABC}$ is a triangle in which altitudes $\mathrm{BE}$ and $\mathrm{CF}$ to sides $\mathrm{AC}$ and $\mathrm{AB}$ are equal (See figure). Show that
(i) $\Delta \mathrm{ABE} \cong \Delta \mathrm{ACF}$
(ii) $\mathrm{AB}=\mathrm{AC}$, i.e., $\mathrm{ABC}$ is an isosceles triangle.

Q5. $\mathrm{ABC}$ and $\mathrm{DBC}$ are two isosceles triangles on the same base $\mathrm{BC}$ (see figure). Show that $\angle \mathrm{ABD}=\angle \mathrm{ACD}$

Q6. $\triangle \mathrm{ABC}$ is an isosceles triangle in which $\mathrm{AB}=\mathrm{AC}$. Side $\mathrm{BA}$ is produced to D such that $\mathrm{AD}=\mathrm{AB}$ (see figure). Show that $\angle \mathrm{BCD}$ is a right angle.

Q7. $\mathrm{ABC}$ is a right angled triangle in which $\angle \mathrm{A}=90^{\circ}$ and $\mathrm{AB}=\mathrm{AC}$. Find $\angle \mathrm{B}$ and $\angle \mathrm{C}$.
Q8. Show that the angles of an equilateral triangle are $60^{\circ}$ each.
Also Read,
Class 9 NCERT Maths Book Chapterwise
Class 9 NCERT Maths Exemplar Chapterwise
Complete Solutions for Class 9 chapter 7 PDF
Class 9 Maths Chapter 6 Exercise 6.1 Solutions Free PDF
Class 9 Maths Chapter 6 Exercise 6.2 Solutions Free PDF
Class 9 Maths Chapter 6 Exercise 6.3 Solutions Free PDF
If you have any Confusion related to NCERT Solutions for Class 9 Maths chapter 7 Exercise 7.2 then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App
Here we have listed Class 9 maths chapter 7 exercise 7.2 solutions in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to score high in your class 9 Maths Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solutions for Class 9 Maths chapter 7 Exercise 7.2 that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
Download The PDF of NCERT Solutions for Class 9 Maths chapter 7 Exercise 7.2 "Triangles"



So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.
All Questions of Chapter 7 Exercise 7.2
Once you complete the chapter 7 then you can revise Ex. 7.2 by solving following questions
Q1. In an isosceles triangle $\mathrm{ABC}$, with $\mathrm{AB}=\mathrm{AC}$, the bisectors of $\angle \mathrm{B}$ and $\angle \mathrm{C}$ intersect each other at $\mathrm{O}$. Join $\mathrm{A}$ to $\mathrm{O}$. Show that : (i) $\mathrm{OB}=\mathrm{OC}$ (ii) AO bisects $\angle \mathrm{A}$.
Q2. In $\triangle \mathrm{ABC}, \mathrm{AD}$ is the perpendicular bisector of $\mathrm{BC}$. Show that $\triangle \mathrm{ABC}$ is an isosceles triangle in which $\mathrm{AB}=\mathrm{AC}$.

Q3. $\mathrm{ABC}$ is an isosceles triangle in which altitudes $\mathrm{BE}$ and $\mathrm{CF}$ are drawn to equal sides $\mathrm{AC}$ and $\mathrm{AB}$ respectively. Show that these altitudes are equal.

Q4. $\mathrm{ABC}$ is a triangle in which altitudes $\mathrm{BE}$ and $\mathrm{CF}$ to sides $\mathrm{AC}$ and $\mathrm{AB}$ are equal (See figure). Show that
(i) $\Delta \mathrm{ABE} \cong \Delta \mathrm{ACF}$
(ii) $\mathrm{AB}=\mathrm{AC}$, i.e., $\mathrm{ABC}$ is an isosceles triangle.

Q5. $\mathrm{ABC}$ and $\mathrm{DBC}$ are two isosceles triangles on the same base $\mathrm{BC}$ (see figure). Show that $\angle \mathrm{ABD}=\angle \mathrm{ACD}$

Q6. $\triangle \mathrm{ABC}$ is an isosceles triangle in which $\mathrm{AB}=\mathrm{AC}$. Side $\mathrm{BA}$ is produced to D such that $\mathrm{AD}=\mathrm{AB}$ (see figure). Show that $\angle \mathrm{BCD}$ is a right angle.

Q7. $\mathrm{ABC}$ is a right angled triangle in which $\angle \mathrm{A}=90^{\circ}$ and $\mathrm{AB}=\mathrm{AC}$. Find $\angle \mathrm{B}$ and $\angle \mathrm{C}$.
Q8. Show that the angles of an equilateral triangle are $60^{\circ}$ each.
Also Read,
Class 9 NCERT Maths Book Chapterwise
Class 9 NCERT Maths Exemplar Chapterwise
Complete Solutions for Class 9 chapter 7 PDF
Class 9 Maths Chapter 6 Exercise 6.1 Solutions Free PDF
Class 9 Maths Chapter 6 Exercise 6.2 Solutions Free PDF
Class 9 Maths Chapter 6 Exercise 6.3 Solutions Free PDF
If you have any Confusion related to NCERT Solutions for Class 9 Maths chapter 7 Exercise 7.2 then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App
Comments
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
