Hey, do you want to learn about the Magnetic Field due to Infinite Straight Conductor? If yes. Then keep reading.

Magnetic field due to long straight conductor

Here we will discuss all the cases involved in the magnetic field due to Conductor such as Magnetic Field due to Infinite Straight Conductor, and many more discussed below:
Consider a long straight conductor XY through which current I is flowing from $X$ to Y. Let $P$ be the observation point at a distance ‘r’ ‘from the conductor XY. Let us consider an infinitesimally small current element $\mathrm{CD}$ of length d\ell. Let s be the distance of $\mathrm{P}$ from the mid-point $\odot$ of the current element. Let $\theta$ be the angle that OP makes with the direction of the current. The magnetic field at $P$ due to the current element $C D$ is

$\mathrm{dB}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{Id} \ell \sin \theta}{\mathrm{s}^{2}}[\text { Biot-Savart’s law }]$ 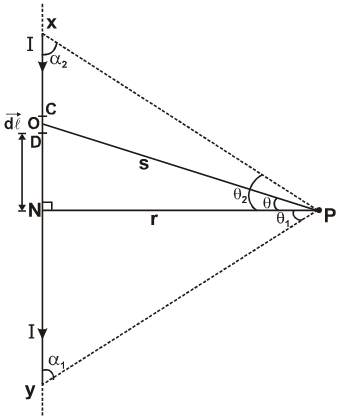The magnetic field at P due to the whole of the conductor XY

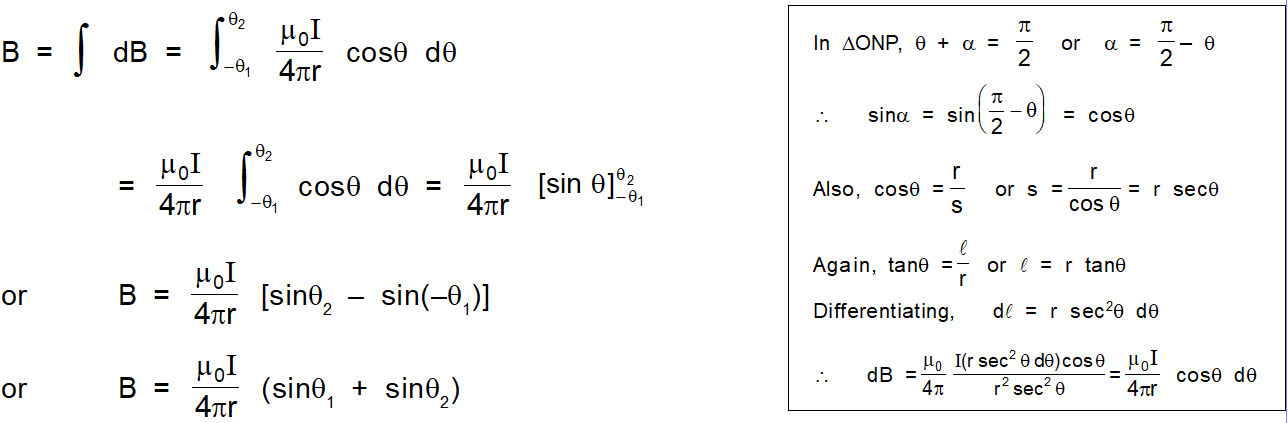
Case I :

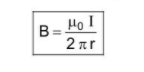
If the conductor is infinitely long, then $\theta_{1}=90^{\circ}$ and $\theta_{2}=90^{\circ}$
$\mathrm{B}=\frac{\mu_{0} \mathrm{I}}{4 \pi}\left[\sin \frac{\pi}{2}+\sin \left(\frac{\pi}{2}\right)\right]=\frac{\mu_{0} \mathrm{I}}{4 \pi \mathrm{r}}[1+1]=\frac{\mu_{0}}{4 \pi} \frac{2 \mathrm{I}}{\mathrm{r}}$ Or

Case II :

If a conductor is of infinite length but one end is in front of point $P$ i.e. one end of conductor starts from point $N$ then $\theta_{1}=0^{\circ}$ and $\theta_{2}=90^{\circ}$                                              

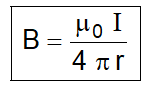
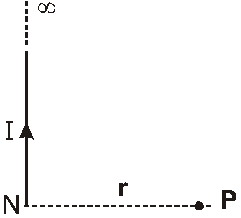
Case III :

Conductor is finite length and point P is just in front of the middle of the conductor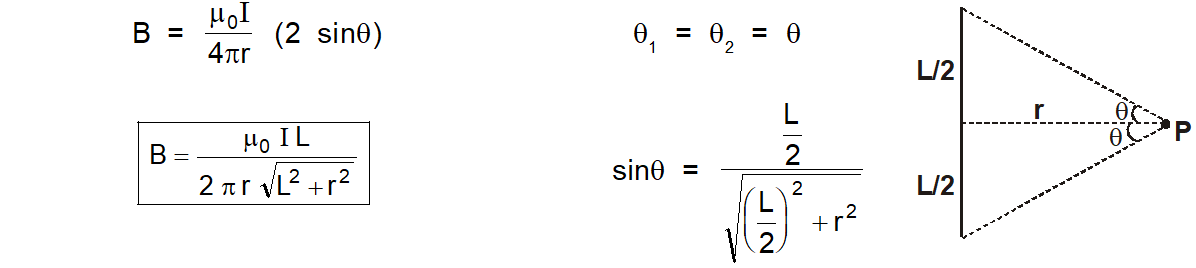

Case IV :

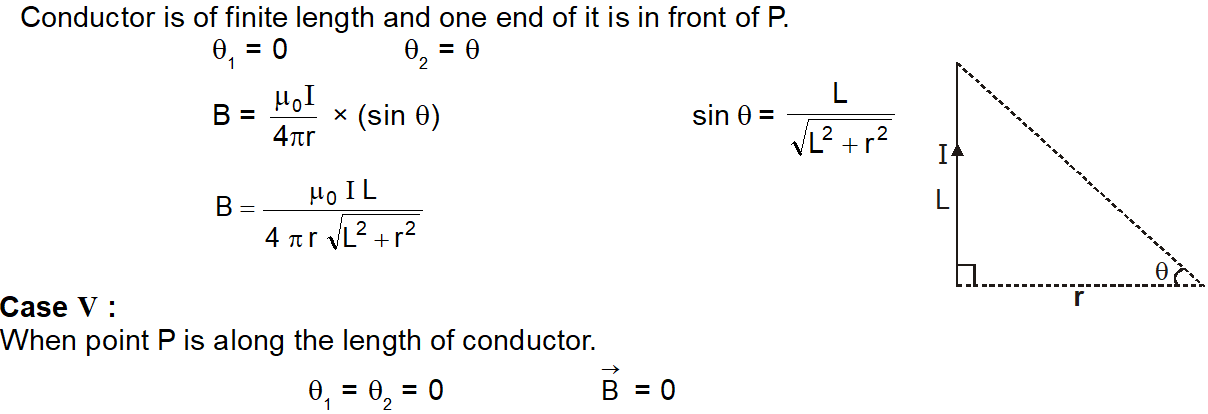
Also Read:
Biot Savart’s Law

Click here for the Video tutorials of Magnetic Effect of Current Class 12

About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depend on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.

For free video lectures and complete study material, Download eSaral APP.