NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.3 - Areas of Parallelograms and Triangles
Class 9Hey, are you a class 9 Student and Looking for Ways to Download NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.3? If Yes then you are at the right place.
Here we have listed Class 9 maths chapter 9 exercise 9.3 solutions in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.
If you want to score high in your class 9 Maths Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.
In this article, we have listed NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.3 that you can download to start your preparations anytime.
So, without wasting more time Let’s start.
India's Best Exam Preparation for Class 9th - Download Now
Download The PDF of NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.3 "Areas of Parallelograms and Triangles"







So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.
India's Best Exam Preparation for Class 9th - Download Now
All Questions of Chapter 9 Exercise 9.3
Once you complete the chapter 9 then you can revise Ex. 9.3 by solving following questions
Q1. In fig, E is any point on median AD of a $\Delta \mathrm{ABC}$. Show that ar $(\mathrm{ABE})=\operatorname{ar}(\mathrm{ACE})$. 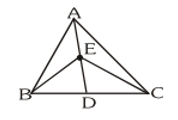
Q2. In a triangle $\mathrm{ABC}, \mathrm{E}$ is the mid-point of median $\mathrm{AD}$. Show that ar $(\mathrm{BED})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC})$.
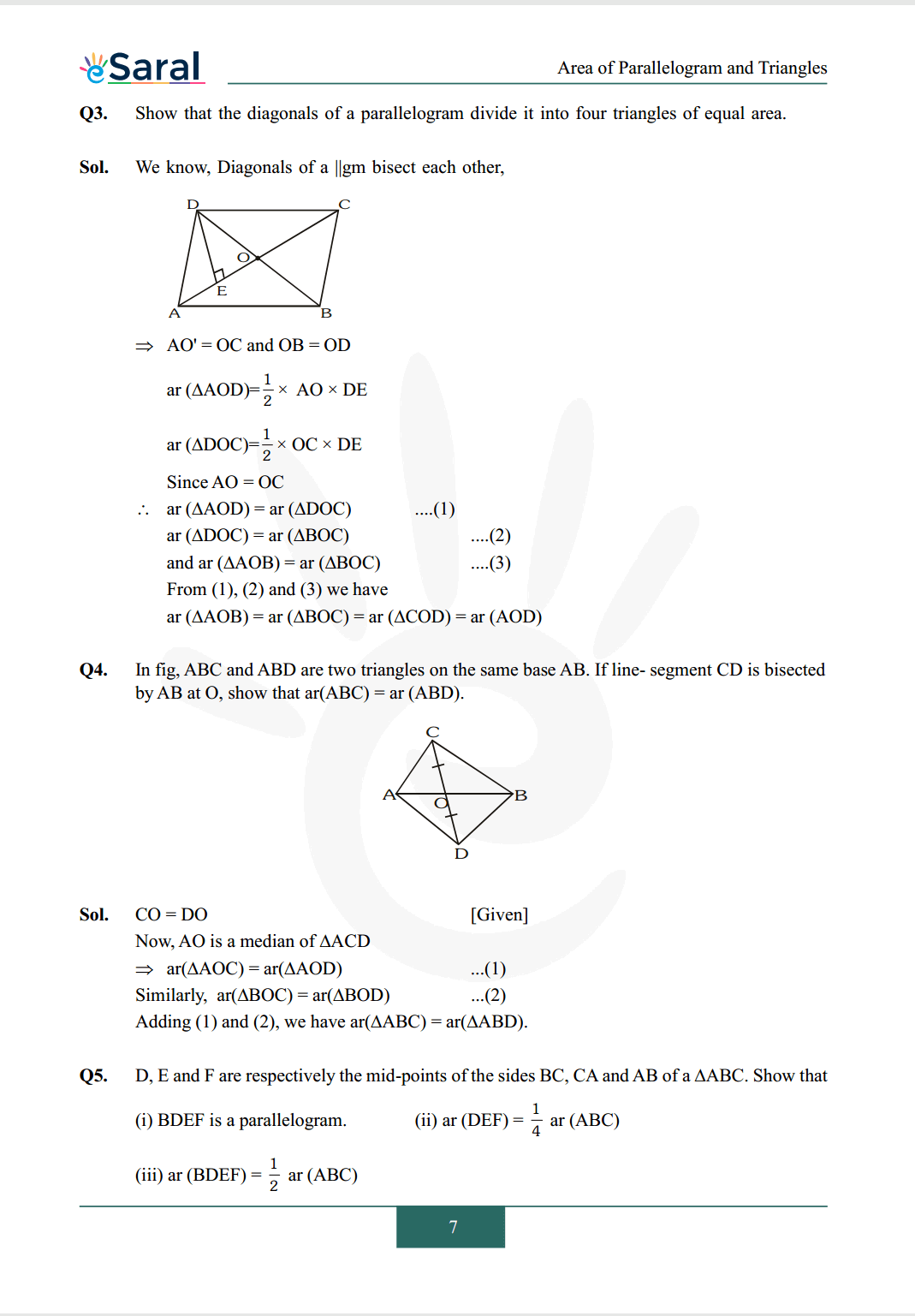
Q3. Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Q4. In fig, $\mathrm{ABC}$ and $\mathrm{ABD}$ are two triangles on the same base $\mathrm{AB}$. If line- segment $\mathrm{CD}$ is bisected by $\mathrm{AB}$ at $\mathrm{O}$, show that $\operatorname{ar}(\mathrm{ABC})=\operatorname{ar}(\mathrm{ABD})$. 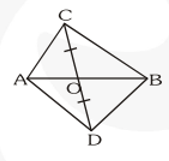
Q5. D, E and $\mathrm{F}$ are respectively the mid-points of the sides $\mathrm{BC}, \mathrm{CA}$ and $\mathrm{AB}$ of $\mathrm{a} \triangle \mathrm{ABC}$. Show that
(i) $\mathrm{BDEF}$ is a parallelogram.
(ii) $\operatorname{ar}(\mathrm{DEF})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC})$
(iii) ar $(\mathrm{BDEF})=\frac{1}{2}$ ar $(\mathrm{ABC})$
Q6. In fig, diagonals AC and BD of quadrilateral ABCD intersect at $\mathrm{O}$ such that $\mathrm{OB}=\mathrm{OD}$. If $\mathrm{AB}=\mathrm{CD}$, then show that : 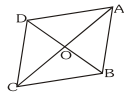
(i) $\operatorname{ar}(\mathrm{DOC})=\operatorname{ar}(\mathrm{AOB})$
(ii) $\operatorname{ar}(\mathrm{DCB})=\operatorname{ar}(\mathrm{ACB})$
(iii) $\mathrm{DA} \| \mathrm{CB}$ or $\mathrm{ABCD}$ is a parallelogram.
Q7. $\mathrm{D}$ and $\mathrm{E}$ are points on sides $\mathrm{AB}$ and $\mathrm{AC}$ respectively of $\Delta \mathrm{ABC}$ such that $\operatorname{ar}(\mathrm{DBC})=\operatorname{ar}(\mathrm{EBC})$. Prove that $\mathrm{DE} \| \mathrm{BC}$.
Q8. $\mathrm{XY}$ is a line parallel to side $\mathrm{BC}$ of a triangle $\mathrm{ABC}$. If $\mathrm{BE} \| \mathrm{AC}$ and $\mathrm{CF} \| \mathrm{AB}$ meet $\mathrm{XY}$ at $\mathrm{E}$ and $F$ respectively, show that ar $(\Delta \mathrm{ABE})=$ ar $(\Delta \mathrm{ACF})$.
India's Best Exam Preparation for Class 9th - Download Now
Q9. The side $A B$ of a parallelogram $A B C D$ is produced to any point $P$. A line through A and parallel to CP meets CB produced at $\mathrm{Q}$ and then parallelogram $\mathrm{PBQR}$ is completed Show that ar $(\mathrm{ABCD})=\operatorname{ar}(\mathrm{PBQR}) .$ 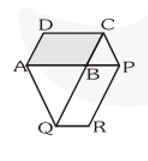
Q10. Diagonals AC and BD of a trapezium $\mathrm{ABCD}$ with $\mathrm{AB} \| \mathrm{DC}$ intersect each other at $\mathrm{O}$. Prove that ar $(\mathrm{AOD})=\operatorname{ar}(\mathrm{BOC})$.
Q11. In fig, $\mathrm{ABCDE}$ is a pentagon. A line through B parallel to 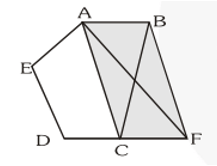
AC meets DC produced at $\mathrm{F}$. Show that
(i) $\operatorname{ar}(\mathrm{ACB})=\operatorname{ar}(\mathrm{ACF})$
(ii) $\operatorname{ar}(\mathrm{AEDF})=\operatorname{ar}(\mathrm{ABCDE})$
Q12. A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Q13. $\mathrm{ABCD}$ is a trapezium with $\mathrm{AB} \| \mathrm{DC}$. A line parallel to $\mathrm{AC}$ intersects $\mathrm{AB}$ at $\mathrm{X}$ and $\mathrm{BC}$ at $\mathrm{Y}$. Prove that ar $(\mathrm{ADX})=\operatorname{ar}(\mathrm{ACY})$.
Q14. In fig, $\mathrm{AP}\|\mathrm{BQ}\| \mathrm{CR}$. Prove that ar $(\mathrm{AQC})=\operatorname{ar}(\mathrm{PBR})$. 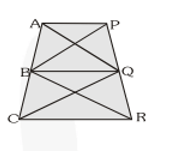
Q15. Diagonals $\mathrm{AC}$ and $\mathrm{BD}$ of a quadrilateral $\mathrm{ABCD}$ intersect at $\mathrm{O}$ in such a way that ar $(\mathrm{AOD})=\operatorname{ar}(\mathrm{BOC})$. Prove that $\mathrm{ABCD}$ is a trapezium.
Q16. In fig, ar $(\mathrm{DRC})=\operatorname{ar}(\mathrm{DPC})$ and ar $(\mathrm{BDP})=\operatorname{ar}(\mathrm{ARC})$. Show that both the quadrilaterals $\mathrm{ABCD}$ and DCPR are trapeziums. 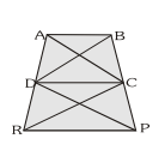
India's Best Exam Preparation for Class 9th - Download Now
Also Read,
Class 9 NCERT Maths Book Free PDF Download
Class 9 NCERT Maths Exemplar Free PDF Download
Complete Solutions for Class 9 Maths chapter 9 Download
Class 9 Maths Chapter 8 Exercise 8.1 Solutions Free Download
Class 9 Maths Chapter 8 Exercise 8.2 Solutions Free Download
If you have any Confusion related to NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.3 then feel free to ask in the comments section down below.
To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
