NCERT Solutions for Class 9 Maths chapter 10 Exercise 10.5 - Circles - Free PDF Download

Hey, are you a class 9 Student and Looking for Ways to Download NCERT Solutions for Class 9 Maths chapter 10 Exercise 10.5? If Yes then you are at the right place.

Here we have listed Class 9 maths chapter 10 exercise 10.5 solutions in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to score high in your class 9 Maths Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.

In this article, we have listed NCERT Solutions for Class 9 Maths chapter 10 Exercise 10.5 that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

Download The PDF of NCERT Solutions for Class 9 Maths chapter 10 Exercise 10.5 "Circles"

So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.

All Questions of Chapter 10 Exercise 10.5

Once you complete the chapter 10 then you can revise Ex. 10.5 by solving following questions

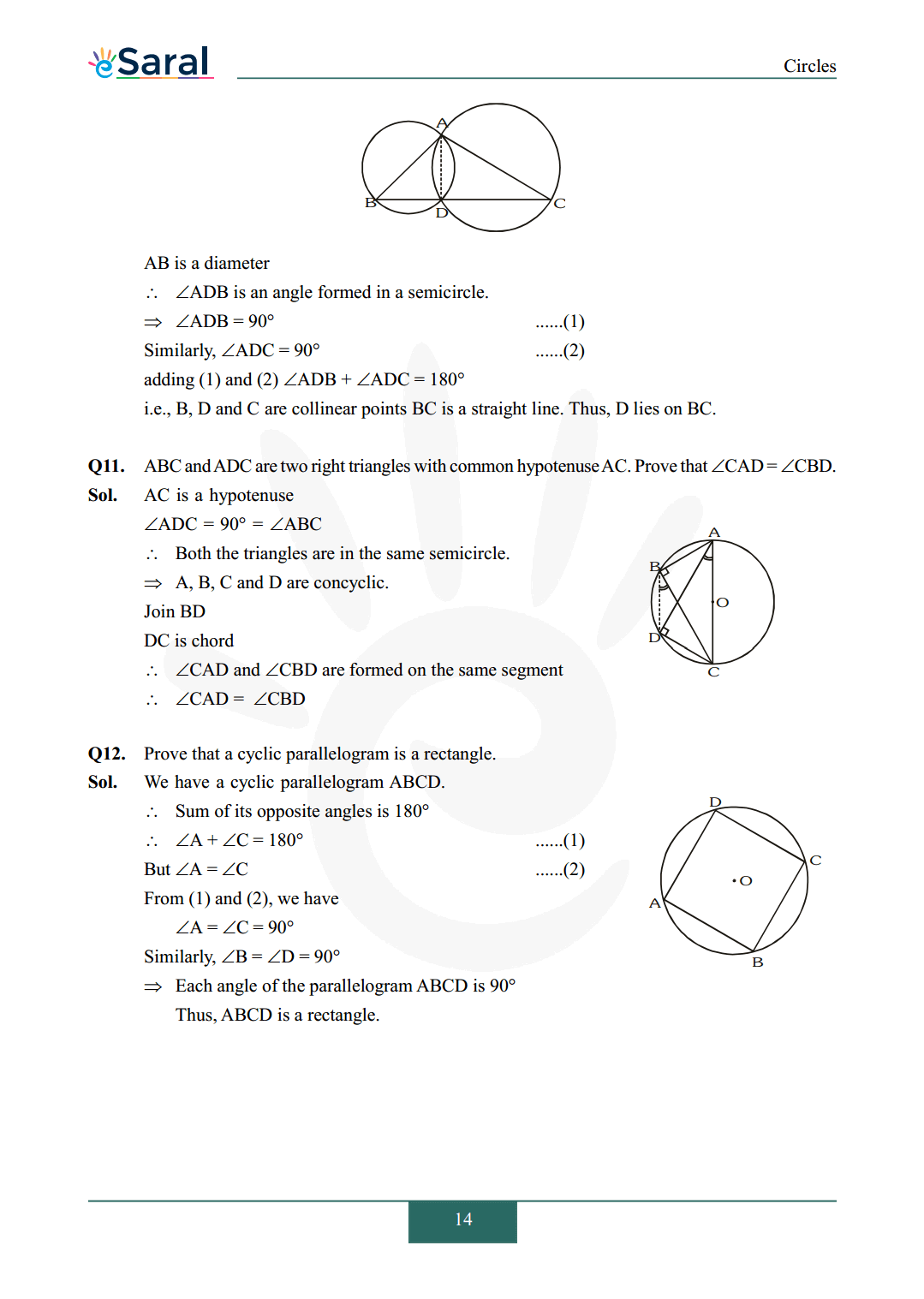
Q1. In Fig. A, B and C are three points on a circle with centre $\mathrm{O}$ such that $\angle \mathrm{BOC}=30^{\circ}$ and $\angle \mathrm{AOB}=60^{\circ} .$ If $\mathrm{D}$ is a point on the circle other than the arc $\angle \mathrm{ABC}$, find $\angle \mathrm{ADC}$.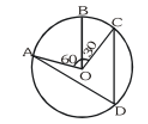

Q2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.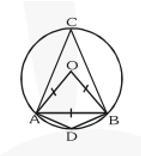


Q3. In figure, $\angle \mathrm{PQR}=100^{\circ}$, where $\mathrm{P}, \mathrm{Q}$ and $\mathrm{R}$ are points on a circle with centre $\mathrm{O}$. Find $\angle \mathrm{OPR}$.


Q4. In fig. $\angle \mathrm{ABC}=69^{\circ}, \angle \mathrm{ACB}=31^{\circ}$, find $\angle \mathrm{BDC}$.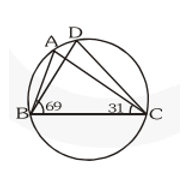


Q5. In figure, $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$ are four points on a circle. AC and BD intersect at a point $\mathrm{E}$ such that $\angle \mathrm{BEC}=130^{\circ}$ and $\angle \mathrm{ECD}=20^{\circ} .$ Find $\angle \mathrm{BAC}$.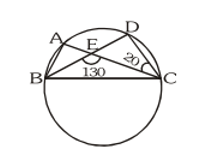


Q6. $\quad \mathrm{ABCD}$ is a cyclic quadrilateral whose diagonals intersect at a point $\mathrm{E}$. If $\angle \mathrm{DBC}=70^{\circ}$, $\angle \mathrm{BAC}=$ is $30^{\circ}$, find $\angle \mathrm{BCD}$. Further, if $\mathrm{AB}=\mathrm{BC}$, find $\angle \mathrm{ECD}$.

Q7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Q8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

Q9. Two circles intersect at two points $\mathrm{B}$ and $\mathrm{C}$. Through $\mathrm{B}$, two line segment $\mathrm{ABD}$ and $\mathrm{PBQ}$ are drawn to intersect the circles at $\mathrm{A}, \mathrm{D}$ and $\mathrm{P}, \mathrm{Q}$ respectively. Prove that $\angle \mathrm{ACP}=\angle \mathrm{QCD}$.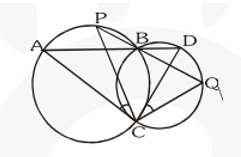


Q10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

Q11. $\mathrm{ABC}$ and $\mathrm{ADC}$ are two right triangles with common hypotenuse $\mathrm{AC}$. Prove that $\angle \mathrm{CAD}=\angle \mathrm{CBD}$.

Q12. Prove that a cyclic parallelogram is a rectangle.

Also Read,

Download NCERT Class 9 Maths Book Free

Download NCERT Class 9 Maths Exemplar Free

Download Complete Solutions for Class 9 Maths chapter 10 PDF

Download Class 9 Maths Chapter 9 Exercise 9.1 Solutions PDF

Download Class 9 Maths Chapter 9 Exercise 9.2 Solutions PDF

Download Class 9 Maths Chapter 9 Exercise 9.3 Solutions PDF 

If you have any Confusion related to NCERT Solutions for Class 9 Maths chapter 10 Exercise 10.5 then feel free to ask in the comments section down below.

To watch Free Learning Videos on Class 9 by Kota’s top Faculties Install the eSaral App