Introduction to Ohm's Law and Resistance | Resistivity | Thermistors

We now have basic idea about Potential difference and Current. Now let us study the relation between them. How potential difference applied across the conductor and current flowing through it are related to each other if certain physical conditions are kept the same. This relation was given by G. S. Ohm in 1828 even before the physical mechanism responsible for flow of current was discovered. We will start with Introduction to Ohm's Law along with resistance, resistivity, specific uses of conducting materials, thermistors. Contents:

1. Introduction to Ohm's Law
2. Ohm's Law & Resistance
3. Resistivity
4. Specific uses of conducting materials
5. Thermistors

Introduction to Ohm's Law

If the physical state i.e. temperature, nature of material and dimensions of a conductor remain unchanged then the ratio of potential difference applied across to ends to current flowing through it remains constant. ${\rm{V}} \propto {\rm{I}}$ or $\quad {\rm{V}} = {\rm{IR}}\quad $ where ${\rm{R}} = {{\rm{V}} \over {\rm{I}}}$ is resistance of conductor. ${\rm{I}} = {\rm{neA}}{{\rm{V}}_{\rm{d}}}$ $ = {\rm{n}}e{\rm{A}}{{{\rm{eE}}} \over {\rm{m}}}\tau $ $ = \left( {{{{\rm{n}}{{\rm{e}}^2}\tau } \over {\rm{m}}}} \right){\rm{AE}}$ $ = \left( {{{{\rm{n}}{{\rm{e}}^2}\tau } \over {\rm{m}}}} \right){\rm{A}}{{\rm{V}} \over {\rm{L}}}$ So, ${\rm{R}} = {{\rm{V}} \over {\rm{I}}} = \left( {{{\rm{m}} \over {{\rm{n}}{{\rm{e}}^2}\tau }}} \right){{\rm{L}} \over {\rm{A}}}$ R is resistance of conductor. This is the basic introduction to Ohm's Law. Let's know more about Ohm's Law and Resistance in detail below.

Ohm's Law & Resistance

The property of a substance due to which it opposes the flow of current through it is called resistance. It is a scalar quantity with unit volt/ampere called ohm $(\Omega )$ Dimensions of ${\rm{R}} = {{\rm{V}} \over {\rm{I}}} = {{\rm{W}} \over {{\rm{qI}}}} = {{{{\rm{M}}^1}{{\rm{L}}^2}{{\rm{T}}^{ - 2}}} \over {{\rm{ATA}}}} = {{\rm{M}}^\prime }{{\rm{L}}^2}{{\rm{T}}^{ - 3}}{{\rm{A}}^{ - 2}}$ The reciprocal of resistance is called conductance ${\rm{G}} = {1 \over {\rm{R}}}$ The SI unit is ohm^-1 or mho or siemen (s) and its dimensions are ${M^{ - 1}}{L^{ - 2}}{{\rm{T}}^3}{{\rm{T}}^2}$. Important Points

1. The substances which obey ohm’s law are called Ohmic or linear conductor. The resistance of such conductors is independent of magnitude and polarity of applied potential difference. Here the graph between I and V is a straight line passing through the origin. The reciprocal of slope of straight line gives resistance ${\rm{R}} = {{\rm{V}} \over {\rm{I}}} = {1 \over {\tan \theta }}$ = constant. Examples: silver, copper, mercury, carbon, mica etc. [caption id="attachment_4563" align="aligncenter" width="165"] 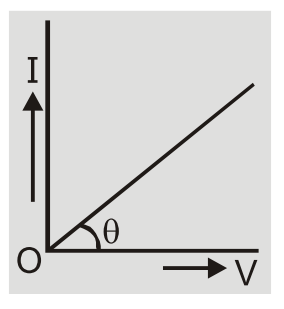I-V graph for Ohmic conductors (which follow Ohm's Law)[/caption]
2. The substances which do not obey ohm’s law are called non-Ohmic or non-linear conductors. The I–V curve is not a straight line. Example: p n diode, transistors, thermionic valves, rectifiers etc. [caption id="attachment_4564" align="aligncenter" width="165"] 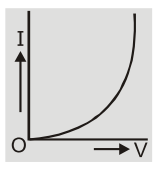I-V graph for non-Ohmic conductors (which doesn't follow Ohm's Law)[/caption]
3. ${\rm{V}} = $ IR defines resistance and hence it is applicable to all ohmic and non-ohmic conductors. If ${\rm{R}}$ is constant or ${\rm{V}} \propto {\rm{I}}$ then it represents ohm's law.
4. The relation ${\rm{R}} = {{\rm{V}} \over {\rm{I}}}$ is macroscopic form while $\rho = {{\rm{E}} \over {\rm{J}}}$ is microscopic form of Ohm's Law.

The resistance of a conductor depends on temperature, nature of material, length and area of cross-section. The temperature dependence of resistance is given by ${\rm{R}} = {{\rm{R}}_0}(1 + \alpha \Delta \theta ),$where $\alpha $ is temperature coefficient of resistance and $\Delta $$\theta $ is change in temperature. The temperature coefficient of resistance $\alpha = {{R - {R_0}} \over {{R_0}\Delta \theta }}$ is defined as change in resistance per unit resistance at $0^{\circ} \mathrm{C}$ per degree rise of temperature. The resistance of a given object depends primarily on two factors: What material it is made of, and its shape. For a given material, the resistance is inversely proportional to the cross-sectional area; for example, a thick copper wire has lower resistance than an otherwise-identical thin copper wire. Also, for a given material, the resistance is proportional to the length; for example, a long copper wire has higher resistance than an otherwise-identical short copper wire. [source] For maximum metals $\alpha = {1 \over {273}} $ per $^{\circ} \mathrm{C}$ so ${\rm{R}} = {{\rm{R}}_0}\left( {1 + {{\Delta \theta } \over {273}}} \right) = {{\rm{R}}_0}\left( {{{273 + \Delta \theta } \over {273}}} \right) = {{\rm{R}}_0}{{\rm{T}} \over {273}}$ So, R $ \propto $ T i.e. the resistance of pure metallic conductor is proportional to its absolute temperature. The fractional change in resistance without change in volume or mass are: (a) When change in length is small $( \le 5\% )$ fractional change in $R$ is ${{\Delta R} \over R} = {{2\Delta L} \over L}$ (b) When change in radius is small $( \le 5\% )$ fractional change in $R$ is ${{\Delta R} \over R} = {{ - 4\Delta r} \over r}$ (c) When change in area is small $( \le 5\% )$ fractional change in $R$ is ${{\Delta R} \over R} = {{ - 2\Delta A} \over A}$

Resistivity

${\rm{R}} \propto {\rm{L}}$ and ${\rm{R}} \propto {1 \over {\rm{A}}}$ So,$\quad {\rm{R}} \propto {{\rm{L}} \over {\rm{A}}}\quad $ or $\quad {\rm{R}} = \rho {{\rm{L}} \over {\rm{A}}}$ where, $\rho $ is called resistivity or specific resistance. In terms of microscopic quantities $E = \rho J$ so resistivity is numerically equal to ratio of magnitude of electric field to current density. $\rho = {{RA} \over L}$ So, if $L = 1{\rm{m}},{\rm{A}} = 1{{\rm{m}}^2}$ then $\rho = {\rm{R}}.$ Specific resistivity is numerically equal to resistance of substance having unit area of cross-section and unit length. It is a scalar with unit ohm-meter $(\Omega - m)$ and dimensions ${M^1 }{L^3}{T^{ - 3}}{{\rm{A}}^{ - 2}}$ . The reciprocal of resistivity is called conductivity or specific conductance with units mho/m and dimensions ${{\rm{M}}^{ - 1}}{{\rm{L}}^{ - 3}}{{\rm{T}}^3}{{\rm{A}}^2},\quad \sigma = {1 \over \rho } = {{{\rm{n}}{{\rm{e}}^2}\tau } \over {\rm{m}}} = $ ne\mu Important Points

1. The resistivity is independent of shape and size of body and depends on nature of material of body. The resistivity is the property of material while resistance is property of object.
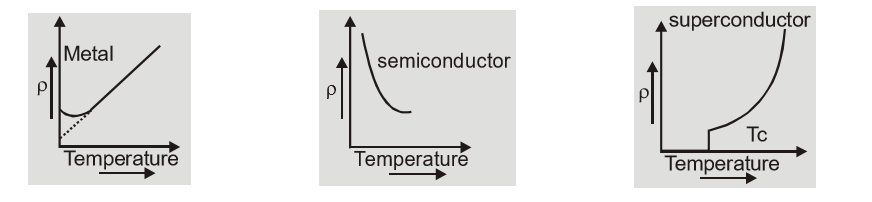
2. The temperature dependence of resistivity is given by relation $\rho = {\rho _0}(1 + \infty \Delta \theta )$ where $ \propto $is temperature coefficient of resistivity and $\Delta \theta $ is change is temperature. For metals $ \propto $ is positive so resistivity increases with temperature while for non-metals $\infty $ is negative so resistivity decreases with temperature.

[caption id="attachment_4566" align="aligncenter" width="543"] Temperature dependence of Resistivity[/caption]

Specific uses of conducting materials

1. The heating element of devices like heater, geyser, press etc. are made of nichrome because it has high resistivity and high melting point. It does not react with air and acquires steady state when red hot at $800^{\circ} \mathrm{C}$ .
2. Fuse wire is made of tin lead alloy because it has low melting point and low resistivity. The fuse is used in series, and melts to produce open circuit when current exceeds the safety limit.
3. Resistances of resistance box are made of Manganin or Constantan because they have moderate resistivity and very small temperature coefficient of resistance. The resistivity is nearly independent of temperature.
4. The filament of bulb is made up of tungsten because it has low resistivity, high melting point of 3300 K and gives light at 2400 K. The bulb is filled with inert gas because at high temperature it reacts with air forming oxide.
5. The connection wires are made of copper because it has low resistance and resistivity.

Thermistors

A thermistor is a heat sensitive device made of semiconducting material where resistivity changes rapidly with change of temperature. It has a large temperature coefficient. The temperature coefficient may be positive or negative. These can be used over wide range of temperature.

Important Applications

1. The thermistors are used to detect small temperature changes because they respond rapidly to temperature changes.
2. The thermistors with a large negative temperature coefficient is used in resistance thermometer in very low temperature measurement.
3. These are used in temperature control units of industry.
4. Thermistors are used in protection of windings of generators, motors and transformers.
5. They are used for voltage stabilization, remote sensing and safe guarding filament of picture tube of T.V.

Also Read:

• Types and Effects of Electric Current
• Combination of Resistances
• EMF and Internal Resistances of a Cell
• Cells Connected in Series, parallel and Mixed
• Kirchhoff’s Circuit Law
• Electric Currents in Conductors
• Wheatstone Bridge
• Post office Box
• Wheatstone Meter Bridge
• Moving Coil galvanometer
• Ammeter and Voltmeter
• Potentiometer Working Principle