Like resistors, a circuit can also have a combination of cells connected in series, parallel or even both! And again like resistors, we can calculate current and voltages that can be replaced by an equivalent cell in a circuit which we will learn here.
A circuit composed solely of components connected in series is known as a series circuit; likewise, one connected completely in parallel is known as a parallel circuit.
In a series circuit, the current that flows through each of the components is the same, and the voltage across the circuit is the sum of the individual voltage drops across each component. In a parallel circuit, the voltage across each of the components is the same, and the total current is the sum of the flowing through each component. [source]
Here we will see cells connected in series, parallel and mixed one by one along with examples.
Contents:
 Cells connected in Series Combination[/caption]
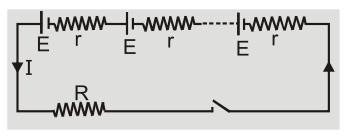
Let 'n' identical cells each of emf E and internal resistance r be connected in series. The combination can be replaced by a single cell of emf nE and internal resistance nr. The current flowing through load ${\rm{I}} = {{{\rm{nE}}} \over {{\rm{R}} + {\rm{nr}}}}$
[caption id="attachment_4616" align="aligncenter" width="205"]
Cells connected in Series Combination[/caption]
Let 'n' identical cells each of emf E and internal resistance r be connected in series. The combination can be replaced by a single cell of emf nE and internal resistance nr. The current flowing through load ${\rm{I}} = {{{\rm{nE}}} \over {{\rm{R}} + {\rm{nr}}}}$
[caption id="attachment_4616" align="aligncenter" width="205"]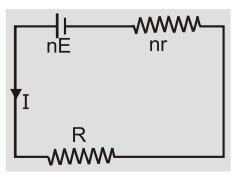 Equivalent circuit for series combination[/caption]
Equivalent circuit for series combination[/caption]
 Cells connected in Parallel Combination[/caption]
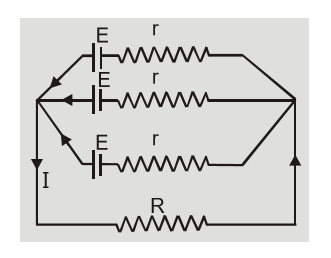
Let ‘m’ identical cells each of emf E and internal resistance r be connected in parallel. The combination can be replaced by a single cell of emf $E$ and internal resistance ${\rm{r}}/{\rm{m}}.$ The current ${\rm{I}} = {{\rm{E}} \over {{\rm{R}} + {\rm{r}}/{\rm{m}}}}$
[caption id="attachment_4618" align="aligncenter" width="218"]
Cells connected in Parallel Combination[/caption]
Let ‘m’ identical cells each of emf E and internal resistance r be connected in parallel. The combination can be replaced by a single cell of emf $E$ and internal resistance ${\rm{r}}/{\rm{m}}.$ The current ${\rm{I}} = {{\rm{E}} \over {{\rm{R}} + {\rm{r}}/{\rm{m}}}}$
[caption id="attachment_4618" align="aligncenter" width="218"]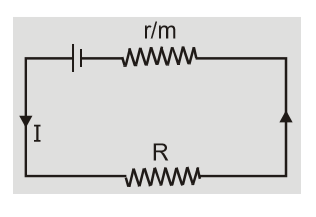 Equivalent circuit for parallel combination[/caption]
Equivalent circuit for parallel combination[/caption]
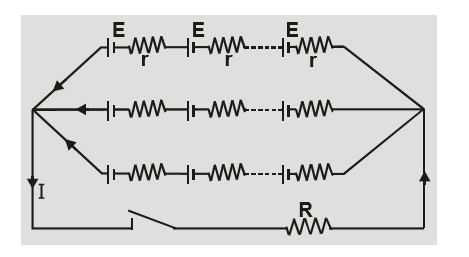 Cells connected in Mixed Grouping[/caption]
[caption id="attachment_4620" align="aligncenter" width="165"]
Cells connected in Mixed Grouping[/caption]
[caption id="attachment_4620" align="aligncenter" width="165"]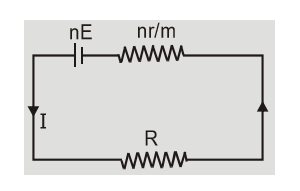 Equivalent circuit for Mixed Grouping[/caption]
Also Read:
Equivalent circuit for Mixed Grouping[/caption]
Also Read:
- Cells connected in Series Combination
- Cells connected in Parallel Combination
- Cells connected in Mixed Grouping
- Solved Examples
Cells connected in Series Combination
The cells are said to be connected in series if negative terminal first is connected to positive of second whose negative terminal is connected to positive of third cell. The external resistance is connected between free terminals of first and last cells. [caption id="attachment_4615" align="aligncenter" width="255"] Cells connected in Series Combination[/caption]
Let 'n' identical cells each of emf E and internal resistance r be connected in series. The combination can be replaced by a single cell of emf nE and internal resistance nr. The current flowing through load ${\rm{I}} = {{{\rm{nE}}} \over {{\rm{R}} + {\rm{nr}}}}$
[caption id="attachment_4616" align="aligncenter" width="205"]
Cells connected in Series Combination[/caption]
Let 'n' identical cells each of emf E and internal resistance r be connected in series. The combination can be replaced by a single cell of emf nE and internal resistance nr. The current flowing through load ${\rm{I}} = {{{\rm{nE}}} \over {{\rm{R}} + {\rm{nr}}}}$
[caption id="attachment_4616" align="aligncenter" width="205"] Equivalent circuit for series combination[/caption]
Equivalent circuit for series combination[/caption]
-
- If ${\rm{nr}} < < {\rm{R}}$ then ${\rm{I}} = {{{\rm{nE}}} \over {\rm{R}}}$ If equivalent internal resistance nr is less than external resistance R then current in circuit is equal to n times circuit current due to single cell.
- If nr >> R then I = E/r. If equivalent internal resistance nr is greater than external resistance R then current in circuit is equal to short circuited current obtained from one cell.
- Maximum current can be drawn from series combination of cells if external resistance is very large as compared to equivalent internal resistance.
- If in series combination of n cells p cells are reversed than equivalent emf${E_{{\rm{eq}}}} = ({\rm{n}} - {\rm{p}}){\rm{E}} - {\rm{pE}} = ({\rm{n}} - 2{\rm{p}}){\rm{E}}\quad $ and $\quad {{\rm{r}}_{{\rm{eq}}}} = {\rm{nr}}\quad $ So current ${\rm{I}} = {{({\rm{n}} - 2{\rm{p}}){\rm{E}}} \over {{\rm{nr}} + {\rm{R}}}}$
- If un-identical cells are connected in series then${E_{{\rm{eq}}}} = {{\rm{E}}_1} + {{\rm{E}}_2} + \ldots . = \Sigma {{\rm{E}}_{\rm{i}}}$ and ${r_{eq}} = {r_1} + {r_2} + \ldots . = \Sigma {r_i}$ So current ${\rm{I}} = {{\Sigma {{\rm{E}}_{\rm{i}}}} \over {{\rm{R}} + \Sigma {{\rm{r}}_{\rm{i}}}}}$.
Cells connected in Parallel Combination
The cells are said to be connected in parallel if positive terminals of all the cells are connected together at one point and their negative terminals at another point. The external resistor is connected between these two points. [caption id="attachment_4617" align="aligncenter" width="237"] Cells connected in Parallel Combination[/caption]
Let ‘m’ identical cells each of emf E and internal resistance r be connected in parallel. The combination can be replaced by a single cell of emf $E$ and internal resistance ${\rm{r}}/{\rm{m}}.$ The current ${\rm{I}} = {{\rm{E}} \over {{\rm{R}} + {\rm{r}}/{\rm{m}}}}$
[caption id="attachment_4618" align="aligncenter" width="218"]
Cells connected in Parallel Combination[/caption]
Let ‘m’ identical cells each of emf E and internal resistance r be connected in parallel. The combination can be replaced by a single cell of emf $E$ and internal resistance ${\rm{r}}/{\rm{m}}.$ The current ${\rm{I}} = {{\rm{E}} \over {{\rm{R}} + {\rm{r}}/{\rm{m}}}}$
[caption id="attachment_4618" align="aligncenter" width="218"] Equivalent circuit for parallel combination[/caption]
Equivalent circuit for parallel combination[/caption]
- If ${\rm{r}}/{\rm{m}} < < {\rm{R}}$ then ${\rm{I}} = {{\rm{E}} \over {\rm{R}}}$ . If equivalent internal resistance ${\rm{r}}/{\rm{m}}$ is less than external resistance ${\rm{R}}$ then current in circuit is equal to current produced by a single cell.
- If ${\rm{r}}/{\rm{m}} > > {\rm{R}}$ then ${\rm{I}} = {{{\rm{mE}}} \over {\rm{r}}}$. If equivalent internal resistance ${{\rm{r}} \over {\rm{m}}}$ is greater than external resistance then current in circuit is equal to ${\rm{m}}$ times the current produced by a short circuited cell.
- Thus maximum current can be drawn from parallel combination of cells if external resistance is small as compared to net internal resistance of cells.
Mixed Grouping
Let there be $n$ identical cells in one row and $m$ rows of cells in parallel. The combination of cells can be replaced by a single cell of emf nE and internal resistance ${{{\rm{ nr }}} \over m}$ . The current $I = {{nE} \over {R + {{nr} \over m}}} = {E \over {{R \over n} + {r \over m}}}$ where $\quad {\rm{n}} \times {\rm{m}} = {\rm{p}} = $ total number of cells. [caption id="attachment_4619" align="aligncenter" width="279"] Cells connected in Mixed Grouping[/caption]
[caption id="attachment_4620" align="aligncenter" width="165"]
Cells connected in Mixed Grouping[/caption]
[caption id="attachment_4620" align="aligncenter" width="165"] Equivalent circuit for Mixed Grouping[/caption]
Equivalent circuit for Mixed Grouping[/caption]
-
- The current in the circuit is maximum when ${{\rm{R}} \over {\rm{n}}} + {{\rm{r}} \over {\rm{m}}}$ is minimum So$\quad {{\rm{d}} \over {{\rm{dm}}}}\left( {{{\rm{R}} \over {\rm{n}}} + {{\rm{r}} \over {\rm{m}}}} \right) = 0\quad $ or $\quad {{\rm{d}} \over {{\rm{dm}}}}\left( {{{{\rm{mR}}} \over {\rm{p}}} + {{\rm{r}} \over {\rm{m}}}} \right) = 0\quad $ or $\quad {{\rm{R}} \over {\rm{p}}} - {{\rm{r}} \over {{{\rm{m}}^2}}} = 0$ or $\quad {{\rm{R}} \over {\rm{p}}} = {{\rm{R}} \over {{\rm{mn}}}} = {{\rm{r}} \over {{{\rm{m}}^2}}}\quad $ or $\quad {{\rm{R}} \over {\rm{n}}} = {{\rm{r}} \over {\rm{m}}}$ In mixed grouping of cells current in circuit is maximum if ${{\rm{R}} \over {\rm{n}}} = {{\rm{r}} \over {\rm{m}}}\quad $ and $\quad {{\rm{I}}_{\max }} = {{{\rm{nE}}} \over {2{\rm{R}}}} = {{{\rm{mE}}} \over {2{\rm{r}}}}$
- In mixed grouping of cells power transferred to the load is maximum where external resistance R is equal to total internal resistance or $R = {{{\rm{ nr }}} \over m}\quad $ or $\quad {R \over n} = {r \over m}$. This shows power transfer is maximum when current is maximum.$P = {{{E^2}R} \over {{{\left( {{R \over n} + {r \over m}} \right)}^2}}}\quad $ and $\quad {P_{\max }} = {{{n^2}{E^2}} \over {4R}} = {{{m^2}{E^2}R} \over {4{r^2}}}$
-
In mixed combination of cells, current in circuit and power transferred to load become maximum under same condition. This is why it is preferred over series and parallel combination of cells.
Solved Examples
Q.Three identical cells each of emf 2V and unknown internal resistance are connected in parallel. This combination is connected to a 5$\Omega $ resistor. If the terminal voltage across the cells is 1.5V. What is the internal resistance of each cell?
Ans.In parallel combination of three cells ${\rm{I}} = {{\rm{E}} \over {{\rm{R}} + {\rm{r}}/3}}$
Terminal potential difference $V = IR = {{ER} \over {R + r/3}}\quad $ or $\quad {r \over 3} = {{ER - RV} \over V}$
or $\quad r = 3\left( {{{ER - RV} \over V}} \right) = 3\left( {{{2 \times 5 - 5 \times 1.5} \over {1.5}}} \right) = 5\Omega $
Q.Determine currents ${{\rm{I}}_1},{{\rm{I}}_2}$ and ${{\rm{I}}_3}?$
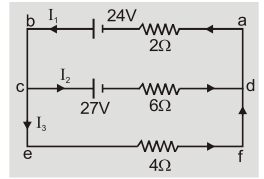

Ans.Using II law in loop abcda $ - 2{{\rm{I}}_1} + 24 - 27 - 6{{\rm{I}}_2} = 0\quad $ or $\quad 2{{\rm{I}}_1} + 6{{\rm{I}}_2} = - 3$ $ \ldots ..(1)$
Using II law in loop cdfec we get $\quad - 27 - 6{{\rm{I}}_2} + 4{{\rm{I}}_3} = 0\quad $ or $\quad - 6{{\rm{I}}_2} + 4{{\rm{I}}_3} = 27\quad \ldots \ldots (2)$
From junction rule at c we get $\quad {{\rm{I}}_1} = {{\rm{I}}_2} + {{\rm{I}}_3}$ $ \ldots ..(3)$
From 2 and 3 we get $\quad - 6{{\rm{I}}_2} + 4\left( {{{\rm{I}}_1} - {{\rm{I}}_2}} \right) = 27\quad $ or $\quad 4{{\rm{I}}_1} - 10{{\rm{I}}_2} = 27\quad \ldots \ldots $ (4)
Solving 1 and 4 we get ${{\rm{I}}_1} = 3{\rm{A}},\quad {{\rm{I}}_2} = - 1.5{\rm{A}}\quad $ so ${{\rm{I}}_3} = {{\rm{I}}_1} - {{\rm{I}}_2} = 4.5{\rm{A}}$
Negative ${{\rm{I}}_2}$ means the direction should have been opposite to shown in figure.
- Types and Effects of Electric Current
- Ohm’s Law and Resistance
- Combination of Resistances
- EMF and Internal Resistances of a Cell
- Cells Connected in Series, parallel and Mixed
- Kirchhoff’s Circuit Law
- Electric Currents in Conductors
- Wheatstone Bridge
- Post office Box
- Wheatstone Meter Bridge
- Moving Coil galvanometer
- Ammeter and Voltmeter
- Potentiometer Working Principle
Comments
Félicité Luise
Aug. 13, 2024, 6:43 p.m.
Hi Team,
I wanted to introduce myself in a way that shows I’m interesting, witty and clever. Alas, I wrote this email instead.
I come bearing just what you’ve always wanted, another pitch! I’ll get this over as quickly as possible.
Are you accepting paid links on your website?
If yes, how much would you charge for this?
If not, will you be interested in a 3-way link exchange that can help boost your website ranking?
Consider my fingers, toes and all appendages crossed!
Cheers,
Félicité Luise
Nomad Hubz
