Potentiometer Working Principle, Uses, Advantages & Disadvantages || Class 12, JEE & NEET
JEE Mains & AdvancedIndia's Best Exam Preparation for Class 12th - Download Now
A potentiometer is a device used to measure the potential difference in a circuit. As we know that potential difference is the amount of work done in bringing a charge from one point to another. When there is potential difference in a circuit, the current flows through the circuit. The Unit of Potential Difference is measured in Volts. The potential difference of a circuit can be measure by a voltmeter. Now we will see Potentiometer Working Principle with the uses of Potentiometer.
Potentiometer Working Principle
The potential drop across any section of wire of uniform cross-section and composition is proportional to length of that section if a constant current flows through it. If $\mathbf{I}$ is the current in potentiometer wire AB of uniform cross-sectional area A, length L and specific resistance $\rho$ then unknown potential difference across AC is $V =\frac{ I \rho \ell}{ A }$ and known potential difference across AB is $E_{p}=\frac{I \rho L}{A}$
India's Best Exam Preparation for Class 12th - Download Now
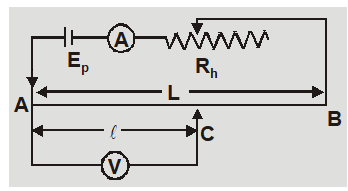
At balance point unknown potential difference = known potential difference or $\frac{V}{\ell}=\frac{E_{p}}{L}$ or $V=\left(\frac{E_{p}}{L}\right) \ell$ or $V=x l$ $$ \text { so } \quad V \propto \ell $$ where x = $E_{p} / L$= potential gradient i.e. fall of potential per unit length of potentiometer. Important Points
India's Best Exam Preparation for Class 12th - Download Now
- Potentiometer was devised by Poggendorf.
- The positive terminals of driving cell and unknown cell must be connected to the same end of potentiometer wire to obtain a balance point.
- A balance point is obtained on potentiometer wire if the fall of potential along potentiometer wire due to driving cell $E_{p}$ is greater than emf of cell to be balanced.
- The diameter of potentiometer wire must be uniform, specific resistance $P$ must be large and temperature coefficient of material of wire must be small.
- It is based of deflection method i.e. while measuring emf it does not draw any current from source of driving emf.
- While measuring unknown potential difference the resistance of potentiometer wire becomes infinite.
India's Best Exam Preparation for Class 12th - Download Now
Browse More Topics Related to Potentiometer:
- Potentiometer Working Principle
- Difference Between Potentiometer and Voltmeter
- Sensitivity of Potentiometer
- Uses of Potentiometer
- Advantages of Potentiometer
- Potentiometer Important Questions
India's Best Exam Preparation for Class 12th - Download Now
Potential Gradient
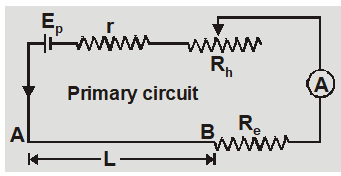
The fall of potential per unit length of potentiometer wire is called potential gradient. r = internal resistance of driving cell; $R_{h}$ = resistance of rheostat, $R_{e}$ = external series resistance, R is resistance of potentiometer wire, L is length of potentiometer wire. The current through primary circuit $I=\frac{E_{p}}{r+R_{h}+R_{e}+R}$
India's Best Exam Preparation for Class 12th - Download Now
The potential gradient $x=\frac{I R}{L}=\frac{E_{p}}{r+R_{h}+R_{e}+R}\left(\frac{R}{L}\right)$
- If $R_{h}$ = 0 and $R_{e}$ = 0 x = $X_{\max }$ = $\frac{E_{p} R}{(r+R) L}0024
- x = $\mathrm{X}_{\mathrm{min}}$ = $\frac{E_{p}}{R+R_{h}+R_{e}+R}\left(\frac{R}{L}\right)$
- $x =\frac{ V }{ L }=\frac{\text { current } \times \text { resistance of potentiometer wire }}{\text { length of potentiometer wire }}= I \left(\frac{ R }{ L }\right)$
- where R/L is resistance per unit length of potentiometer wire.
- $R=\frac{\rho L}{A}$ or $\frac{ R }{ L }=\frac{\rho}{ A }$ so $x =\frac{ I \rho}{ A }=\frac{ I \times \text { specific resistance of material }}{\text { area of cross - sec tion }}$
- Unit of potential gradient is volt/meter and dimensions are $M^{1} L^{1} T^{-3} A^{-1}$.
- The potential gradient depends only on primary circuit and is independent of secondary circuit.
- On increasing the temperature of potentiometer wire there is no change in potential gradient if a constant current is maintained. If current is altered due to change in resistance of wire then potential gradient will change.
- Keeping the thickness of potentiometer wire constant if the length is changed from $L_{1}$ to $L_{2}$ then ratio of potential gradient will be $\frac{x_{1}}{x_{2}}=\frac{L_{2}}{L_{1}}$
- If two wires of length $\mathrm{L}_{1}$ and $\mathrm{L}_{2},$ resistances $\mathrm{R}_{1}$ and $\mathrm{R}_{2}$ are joined in series with a battery of emf $E_{p}$ and a rheostat than the ratio of potential gradients can be calculated as $x_{1}=\left(\frac{E_{p}}{R_{1}+R_{2}}\right) \frac{R_{1}}{L_{1}} \quad$ and $\quad x_{2}=\left(\frac{E_{p}}{R_{1}+R_{2}}\right) \frac{R_{2}}{L_{2}} \quad$ or $\quad \frac{x_{1}}{x_{2}}=\frac{R_{1}}{R_{2}} \cdot \frac{L_{2}}{L_{1}}$
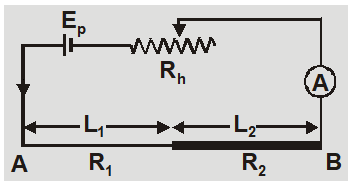
The potential gradient depends on:
- emf of battery in primary circuit $\left(E_{p}\right)$ and its internal resistance (r).
- Length of Potentiometer wire (L), its radius and its resistance (R).
- Specific resistance of material of wire $(\rho)$.
- Current flowing through the wire.
- Additional resistance like resistance of rheostat $\left(R_{h}\right)$ and series external resistance $\left(\mathrm{R}_{\mathrm{e}}\right)$.
India's Best Exam Preparation for Class 12th - Download Now
Watch out the Video: Applications of Potentiometer & its Construction by Saransh Sir.
Also Read:
- Types and Effects of Electric Current
- Ohm’s Law and Resistance
- Combination of Resistances
- EMF and Internal Resistances of a Cell
- Cells Connected in Series, parallel and Mixed
- Kirchhoff’s Circuit Law
- Electric Currents in Conductors
- Wheatstone Bridge
- Post office Box
- Wheatstone Meter Bridge
- Moving Coil galvanometer
- Ammeter and Voltmeter
- Potentiometer Working Principle
