Electric Currents in Conductors | Mobility

We now know an electric charge experiences a force when placed in electric field, if it starts to move it constitutes Electric Current. Here we are going to study the Electric Currents in Conductors when there is no electric field and when the conductor is placed in electric field. We will also learn about Mobility of charge carriers in the end. Contents:

1. Introduction to Conductors & Insulators
2. Electric Currents in Conductors
   1. Behavior of a Conductor in absence of applied Potential Difference
   2. Behavior of a Conductor in presence of applied Potential Difference
3. Mobility

Introduction to Conductors & Insulators

In an atom or a molecule, negatively charged electrons are strongly held by positively charged nucleus therefore the charges are bound to each other and are not free to move. But free charge particles do exist in upper strata of atmosphere called the ionosphere.

Matter is made up of molecules like a small water droplet contains approx 10¹⁹ molecules.

These molecules are closely packed such that the electrons are not attached to only one nuclei. In some materials, these electrons do not move even when electric field is applied, such materials are called insulators.

While in some materials (generally metals), some electrons are allowed free movement inside that material. These are known as conductors, they form electric currents in them when electric field is applied.

Although an electrical insulator is ordinarily thought of as a nonconducting material, it is in fact better described as a poor conductor or a substance of high resistance to the flow of electric current. Different insulating and conducting materials are compared with each other in this regard by means of a material constant known as resistivity. Electrical insulators are used to hold conductors in position, separating them from one another and from surrounding structures. They form a barrier between energized parts of an electric circuit and confine the flow of current to wires or other conducting paths as desired. [source]

Here we will be studying in details about Electric currents in conductors.

A few important points about conductors:

1. Conductors are substances through which electric charges can flow easily.
2. They are characterized by presence of a large number of free electrons $({10^{29}}$ electrons per m³)
3. The number density of free electrons in a conductor is same throughout the conductor. This is because free electrons experience repulsive force between them and conductor allows movement of free electrons. Thus, free electrons are evenly scattered throughout the volume of conductor.
4. These free electrons transport electric charge so are called as Conduction electrons.

Electric Current in Conductors with or without Electric field

a) Behavior of Conductor in absence of applied Potential Difference

1. The free electrons present in a conductor gain energy surrounding and move randomly in a conductor.
   
   [caption id="attachment_4555" align="aligncenter" width="251"] 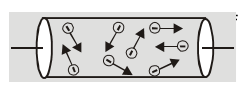Random movement of free electrons in a conductor[/caption]
2. The speed gained by virtue of temperature is called as thermal speed of an electron.${1 \over 2}{\rm{mv}}_{{\rm{ms}}}^2 = {3 \over 2}{\rm{kT}}\quad $
   
   So, Thermal speed $\quad {{\rm{v}}_{{\rm{ms}}}} = \sqrt {{{3{\rm{kT}}} \over {\rm{m}}}} $ where ${\rm{m}}$ is mass of electron.
   
   At room temperature $T = 300{\rm{K}}\quad {{\rm{v}}_{{\rm{rms}}}} = {10^5}{\rm{m}}/{\rm{sec}}$
    
3. The average distance traveled by a free electron between two consecutive collisions is called as Mean Free Path $\lambda .\left(\lambda-10 \mathrm{A}^{\circ}\right)$
   
   Mean free path $\lambda = {{{\rm{ total distance travelled }}} \over {{\rm{ number of collisions }}}}$
   [caption id="attachment_4556" align="aligncenter" width="226"] 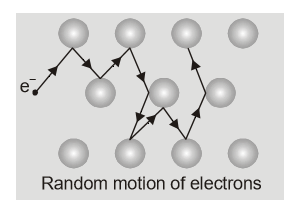Collision of electrons due to random movement[/caption]  
4. The time taken by an electron between two successive collisions is called as Relaxation time. 
   
   $\tau .\left( {\tau - {{10}^{ - 14}}{\rm{s}}} \right)$Relaxation time $\tau = {{{\rm{ total time taken }}} \over {{\rm{ number of collisions }}}}$
5. The thermal speed can be written as ${v_T} = {\lambda \over \tau }$
6. In absence of applied potential difference electrons have random motion. The average displacement and average velocity is zero. There is no flow of current due to thermal motion of free electrons in a conductor.

b) Behavior of Conductor in presence of applied Potential Difference

1. When two ends of conductors are joined to a battery then one end is at higher potential and another at lower potential. This produces an electric field inside the conductor from point of higher to lower potential i.e. $E = {v \over L}$
   
   [caption id="attachment_4557" align="aligncenter" width="290"]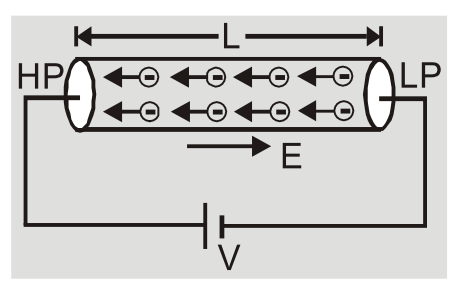 Conductors when battery is connected[/caption]  
2. The field exerts an electric force on free electrons causing acceleration of each electron.$\overrightarrow {\rm{F}} = {\rm{m}}\overrightarrow {\rm{a}} = - {\rm{e}}\overrightarrow {\rm{E}} $ So acceleration $\vec a = {{ - e\vec E} \over m}$
3. The average velocity with which the free electrons are drifted towards the positive end of a conductor under the influence of an external electric field is called drift velocity v_d.Using $\quad \vec v = \vec u + \vec a{\rm{t}}\quad $ we have ${{\vec{v}}_{d}}=\frac{-e\vec{E}}{m}\tau $$\left( {{v_d}~{{10}^{ - 4}}m/sec} \right)$
4. The direction of drift velocity for electrons in a metal is opposite to that of applied field E.
5. Relation between current and drift velocity  Let 'n' be the number density of free electrons and A be the area of cross-section of the conductor.Number of free electrons in a conductor of length L = nAL
   
   Total charge on these free electrons $\Delta {\rm{q}} = $ neAl
   
   Current ${\rm{I}} = {{\Delta {\rm{q}}} \over {\Delta {\rm{t}}}} = {\rm{neAL}}{{{{\rm{v}}_{\rm{d}}}} \over {\rm{L}}} = {\rm{neA}}{{\rm{v}}_{\rm{d}}}$
   
   or $\quad {\rm{I}} = {\rm{neA}}{{\rm{v}}_{\rm{d}}}$
   
   The current flowing through a conductor is directly proportional to the drift velocity $\left( {{\rm{I}} \propto {{\rm{v}}_{\rm{d}}}} \right)$
6. The current density ${\rm{J}} = {{\rm{I}} \over {\rm{A}}} = {\rm{ne}}{{\rm{v}}_{\rm{d}}} = {\rm{ne}}\left( {{{{\rm{eE}}} \over {\rm{m}}}} \right)\tau = \left( {{{{\rm{n}}{{\rm{e}}^2}\tau } \over {\rm{m}}}} \right){\rm{E}}$So, $\quad J \propto E\quad $ or $\quad J = \sigma E$
   
   where, $\sigma = {{{\rm{n}}{{\rm{e}}^2}\tau } \over {\rm{m}}}$ is specific conductivity of conductor which depends on temperature and nature of material.
   
   $\vec J = \sigma \vec E$ is a microscopic form of ohm's law.
7. The drift velocity depends on the nature of metal through $\tau $, applied potential difference, length of the conductor.${v_d} = {{eE} \over m}\tau = {{eV} \over {mL}}\tau $
   ${{\rm{v}}_{\rm{d}}}$ is independent of radius or area of cross-section of a conductor.
8. The rise of temperature causes increase in ${{\rm{v}}_{{\rm{ms}}}}$ and hence a decrease in $\lambda $ and relaxation time $\tau $ causing a decrease in drift velocity.

Mobility

Conductivity arises from mobile charge carriers like electrons in metals, positively charged ions, and electrons in an ionized gas, positive and negative ions in an electrolyte. So there must be some difference in the movement of these different charge carriers. It is called Mobility.   Mobility of a charge carrier is defined as drift velocity acquired per unit electric field. Mobility $\mu = {{{v_d}} \over E} = {{e\tau } \over m} = {e \over m}{{m\sigma } \over {n{e^2}}} = {\sigma \over {ne}}$

The unit is ${m^2}{V^{ - 1}}{s^{ - 1}}$ and dimensions are ${M^{ - 1}}{T^2}{A^1}$

  The mobility depends on applied potential difference, length of conductor, number density of charge carriers, current in conductor, area of cross-section of conductor.

Mobility $\mu = {{{v_d}} \over E} = {{e\tau } \over m} = {e \over m}{{m\sigma } \over {n{e^2}}} = {\sigma \over {ne}}$

The unit is ${{\rm{m}}^2}{{\rm{V}}^{ - 1}}{{\rm{s}}^{ - 1}}$ and dimensions are ${{\rm{M}}^{ - 1}}{{\rm{T}}^2}{{\rm{A}}^1}$

The mobility depends on applied potential difference, length of conductor, number density of charge carriers, current in conductor, area of cross-section of conductor.

    Also Read:

• Types and Effects of Electric Current
• Ohm’s Law and Resistance
• Combination of Resistances
• EMF and Internal Resistances of a Cell
• Cells Connected in Series, parallel and Mixed
• Kirchhoff’s Circuit Law
• Electric Currents in Conductors
• Wheatstone Bridge
• Post office Box
• Wheatstone Meter Bridge
• Moving Coil galvanometer
• Ammeter and Voltmeter
• Potentiometer Working Principle