Here are the Potentiometer Questions for NEET, IIT JEE and Board Exams.
Ex. No current flows if the terminals of a cell are joined with 125 cm length of potentiometer wire. If a 20 resistance is connected in parallel to cell balancing length is reduced by 25 cm. Find internal resistance of cell. Sol. $r=\frac{\ell_{1}-\ell_{2}}{\ell_{2}} \times R =\frac{125-100}{100} \times 20=5 \Omega$
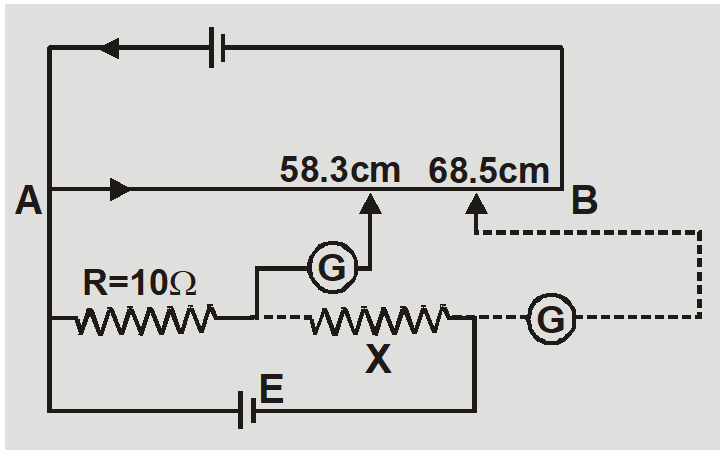
Ex. Figure shows use of potentiometer for comparision of two resistances. The balance point with standard resistance R = 10 is at 58.3 cm, while that with unknown resistance X is 68.5 cm. Find X.
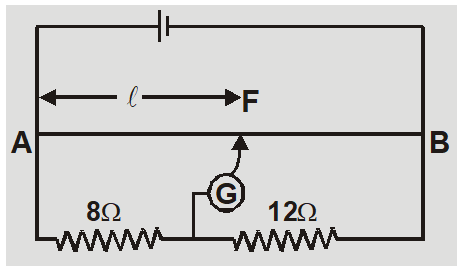
Ex. The length of potentiometer wire is 40cm. Zero deflection in galvanometer is obtained at point F. Find the balancing length AF. Sol. Let x be potential gradient and $V_{1}$ and $V_{2}$ be potential difference across 8$\Omega$ and 12$\Omega$ respectively. $\frac{V_{1}}{V_{2}}=\frac{8}{12}=\frac{x \ell}{x(40-\ell)}$ or $\frac{l}{40-l}=\frac{2}{3}$ or $\ell=16 cm$
Ex. If the current in the primary circuit of a potentiometer wire is 0.2 A, specific resistance of material of wire is $40 \times 10^{-8} \Omega m$ and area of cross-section is $0.8 \times 10^{-6} m ^{2}$ Calculate potential gradient? Sol. Potential gradient $x=\frac{V}{L}=\frac{I R}{L}=\frac{I \rho}{A}=\frac{0.2 \times 40 \times 10^{-8}}{0.8 \times 10^{-6}}=0.1$ volt $/ m$
Ex. A battery of emf 2V is connected in series with a resistance box and a 10m long potentiometer with resistance $1 \Omega / m$. A 10 mV potential difference is balanced across the entire length of wire. Calculate the current flowing in wire and resistance in resistance box. Sol. Potential gradient $x=\frac{E}{r+R+R_{e}}\left(\frac{R}{L}\right)=\frac{2}{0+10+R_{e}} \times 1=\frac{2}{10+R_{e}}$ Potential difference $V=x l$ or $10 \times 10^{-3}=\frac{2}{10+ R _{ e }} \times 10$ or $R_{e}=1990 \Omega$ Current flowing $I=\frac{E}{R+R_{e}}=\frac{2}{10+1990}=1 m A$
Ex. While measuring the potential difference between the terminals of a resistance wire the balance point is obtained at 78.4 cm. The same potential difference is measured as 1.2 V with voltmeter. If standard cell of emf 1.018 V is balanced at 63.2 cm then find error in reading of voltmeter. Sol. $E_{0}=x l_{0}$ and $V=x \ell$ or $V=\frac{E_{0}}{\ell_{0}} \ell$ $V=\frac{1.018 \times 78.4}{63.2}=1.26 volt$ $V=\frac{1.018 \times 78.4}{63.2}=1.26 volt$ so error = 1.2 – 1.26 = –0.06 V
Potentiometer Questions for NEET, IIT JEE and Board Exams
Ex. In the primary circuit of a potentiometer a battery of $2 \mathrm{V}$ and a rheostat of $22 \Omega$ are connected. If the length of potentiometer wire is $10 \mathrm{m}$ and its resistance is $18 \Omega$ then find the potential gradient in wire. Sol. The potential gradient $x=\left(\frac{E}{r+R+R_{h}+R_{e}}\right) \frac{R}{L} \quad r=R_{e}=0 \Omega$ So $x=\left(\frac{2}{0+18+22+0}\right) \frac{18}{10}=0.09 V / m$Ex. No current flows if the terminals of a cell are joined with 125 cm length of potentiometer wire. If a 20 resistance is connected in parallel to cell balancing length is reduced by 25 cm. Find internal resistance of cell. Sol. $r=\frac{\ell_{1}-\ell_{2}}{\ell_{2}} \times R =\frac{125-100}{100} \times 20=5 \Omega$
Ex. Figure shows use of potentiometer for comparision of two resistances. The balance point with standard resistance R = 10 is at 58.3 cm, while that with unknown resistance X is 68.5 cm. Find X.
Browse More Topics Related to Potentiometer:
- Potentiometer Working Principle
- Difference Between Potentiometer and Voltmeter
- Uses of Potentiometer
- Advantages of Potentiometer
- Potentiometer Important Questions
Ex. The length of potentiometer wire is 40cm. Zero deflection in galvanometer is obtained at point F. Find the balancing length AF. Sol. Let x be potential gradient and $V_{1}$ and $V_{2}$ be potential difference across 8$\Omega$ and 12$\Omega$ respectively. $\frac{V_{1}}{V_{2}}=\frac{8}{12}=\frac{x \ell}{x(40-\ell)}$ or $\frac{l}{40-l}=\frac{2}{3}$ or $\ell=16 cm$
Ex. If the current in the primary circuit of a potentiometer wire is 0.2 A, specific resistance of material of wire is $40 \times 10^{-8} \Omega m$ and area of cross-section is $0.8 \times 10^{-6} m ^{2}$ Calculate potential gradient? Sol. Potential gradient $x=\frac{V}{L}=\frac{I R}{L}=\frac{I \rho}{A}=\frac{0.2 \times 40 \times 10^{-8}}{0.8 \times 10^{-6}}=0.1$ volt $/ m$
Ex. A battery of emf 2V is connected in series with a resistance box and a 10m long potentiometer with resistance $1 \Omega / m$. A 10 mV potential difference is balanced across the entire length of wire. Calculate the current flowing in wire and resistance in resistance box. Sol. Potential gradient $x=\frac{E}{r+R+R_{e}}\left(\frac{R}{L}\right)=\frac{2}{0+10+R_{e}} \times 1=\frac{2}{10+R_{e}}$ Potential difference $V=x l$ or $10 \times 10^{-3}=\frac{2}{10+ R _{ e }} \times 10$ or $R_{e}=1990 \Omega$ Current flowing $I=\frac{E}{R+R_{e}}=\frac{2}{10+1990}=1 m A$
Ex. While measuring the potential difference between the terminals of a resistance wire the balance point is obtained at 78.4 cm. The same potential difference is measured as 1.2 V with voltmeter. If standard cell of emf 1.018 V is balanced at 63.2 cm then find error in reading of voltmeter. Sol. $E_{0}=x l_{0}$ and $V=x \ell$ or $V=\frac{E_{0}}{\ell_{0}} \ell$ $V=\frac{1.018 \times 78.4}{63.2}=1.26 volt$ $V=\frac{1.018 \times 78.4}{63.2}=1.26 volt$ so error = 1.2 – 1.26 = –0.06 V
Watch out the Video: Applications of Potentiometer & its Construction by Saransh Sir.
Complete Physics Revision Series by Saransh Sir (AIR 41 in IIT-JEE)
Also Read:
- Types and Effects of Electric Current
- Ohm’s Law and Resistance
- Combination of Resistances
- EMF and Internal Resistances of a Cell
- Cells Connected in Series, parallel and Mixed
- Kirchhoff’s Circuit Law
- Electric Currents in Conductors
- Wheatstone Bridge
- Post office Box
- Wheatstone Meter Bridge
- Moving Coil galvanometer
- Ammeter and Voltmeter
